云南省保山市2019-2020学年八年级上学期数学11月月考试卷

试卷更新日期：2020-09-08 类型：月考试卷

进入出卷网下载

一、填空题

1. 因式分解：x²﹣1＝.

查看试题解析
2. 在△ABC中，∠A=80°，∠B=∠C ，则∠B= ．

查看试题解析
3. 如图，已知 $A B = B C$ ，要使 $Δ A B D ≅ Δ C B D$ ，还需添加一个条件，则可以添加的条件是。（只写一个即可，不需要添加辅助线）

查看试题解析
4. 已知，点M（a，b）与点N（-3，-1）关于x轴对称，则a+b的值是.

查看试题解析
5. 如图，在△ABC中，∠B=∠C=60°，点D在AB边上，DE⊥AB，并与AC边交于点E.如果AD=1，BC=6，那么CE等于.

查看试题解析
6. 在平面直角坐标系中，已知A（-1，1），B（1，1），若要在x轴上找一点P，使AP+BP最短，则点P的坐标为.

查看试题解析

二、选择题

7. 低碳环保理念深入人心，共享单车已成为出行新方式 $.$ 下列共享单车图标（不考虑外围方框），是轴对称图形的是 $($ $)$

A、 B、 C、 D、

查看试题解析
8. 下列运算正确的是（）

A、 ${(π - 3.14)}^{0} = 0$ B、 ${(m - n)}^{2} = m^{2} - n^{2}$ C、 $2 x^{3} \div 2 x^{2} = 2 x$ D、 ${(- b^{2})}^{3} = - b^{6}$

查看试题解析
9. 如图，已知△ABC≌△DCB，AB=10，∠A=80°，∠ABC=60°，那么下列结论中错误的是（）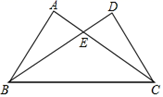

A、∠D=80° B、∠DBC=40° C、AC=DB D、BC=10

查看试题解析
10. 若x²-mx + 1是完全平方式，则m =（）

A、2 B、-2 C、±2 D、±4

查看试题解析
11. 如图，在△ABC中，∠ACB＝90°，分别以点A和点C为圆心，以大于 $\frac{1}{2}$ AC的长为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交AC于点E，连接CD．若∠B＝34°，则∠BDC的度数是（）

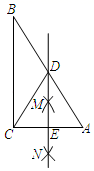A、68° B、112° C、124° D、146°

查看试题解析
12. 已知a＋b=10，ab=6，则a²b+ab²的值为（）

A、120 B、80 C、60 D、40

查看试题解析
13. 如图，五边形ABCDE中，AB∥CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则∠1+∠2+∠3=（）

A、200° B、180° C、160° D、120°

查看试题解析
14. 按一定规律排列的单项式：x³ ，－x⁵ ， x⁷ ，－x⁹ ， x¹¹ ， ……第n个单项式是（）

A、(－1)ⁿ^－¹x²ⁿ^－¹ B、(－1)ⁿx²ⁿ^－¹ C、(－1)ⁿ^－¹x²ⁿ^＋¹ D、(－1)ⁿx²ⁿ^＋¹

查看试题解析

三、解答题

15. 计算：

(1)、 ${(- 2 x^{2})}^{3} + 2 x^{2} \cdot x^{4}$

(2)、 $5 x^{2} y^{3} z - 2 x^{2} y (3 x y^{2} z - 2 y^{2} z)$

查看试题解析
16. 因式分解：

(1)、 $2 x (a - b) + 3 y (b - a)$

(2)、 $3 x^{2} - 12 x + 12$

查看试题解析
17. 先化简，再求值： ${(a + 3)}^{2} - (a + 1) (a - 1) - 2 (2 a + 4)$ ，其中 $a = - \frac{1}{2}$ ．

查看试题解析
18. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）.

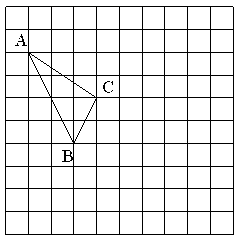
⑴请在如图所示的网格平面内作出平面直角坐标系；
⑵请作出△ABC关于y轴对称的△A′B′C′；
⑶写出点B′的坐标.

查看试题解析
19. 如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证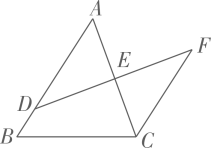： $Δ A D E ≅ C F E$

查看试题解析
20. 证明命题“角的平分线上的点到角两边的距离相等”，要根据题意，画出图形，并用几何符号语言表示已知和求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证.

已知：如图，∠AOC=∠BOC，点P在OC上，PD⊥OA，_▲_.

求证：_▲_.

请你补全已知和求证，并写出证明过程.

查看试题解析
21. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F.

(1)、求∠F的度数；

(2)、若CE=4，求DF的长.

查看试题解析
22. 如图，D是△ABC的BC边上的一点，AD=BD，∠ADC=80°.

(1)、求∠B的度数；

(2)、若∠BAC=70°，判断△ABC的形状，并说明理由.

查看试题解析
23. 如图，在△ABC中，∠BAC=90°，AB=AC.点D从点B出发沿射线BC移动，以AD为边在AB的右侧作△ADE，且∠DAE=90°，AD=AE.连接CE.

(1)、如图1，若点D在BC边上，则∠BCE=度；

(2)、如图2，若点D在BC的延长线上运动.
①∠BCE的度数是否发生变化？请说明理由；

②若BC=6，CD=2，求△ADE的面积.

查看试题解析