辽宁省抚顺市新抚区2020届九年级上学期数学第一次月考试卷

试卷更新日期：2020-09-07 类型：月考试卷

进入出卷网下载

一、单选题。

1. 下列关于x的方程是一元二次方程的是（）

A、x²+1＝0 B、x+ $\frac{1}{x}$ ＝1 C、ax²+bx+c＝0 D、（x+1）（x﹣1）＝x²+x+1

查看试题解析
2. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 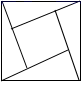B、 C、 D、

查看试题解析
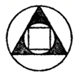3. 方程x²=1的根是（　　）

A、x=1 B、x=﹣1 C、x₁=1，x₂=0 D、x₁=1，x₂=﹣1

查看试题解析
4. 如图，将木条a，b与c钉在一起，∠1＝85°，∠2＝50°，要使木条a与b平行，木条a旋转的度数至少是（）

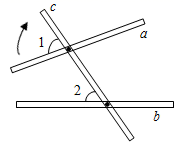A、15° B、25° C、35° D、50°

查看试题解析
5.
如图，△ABC为钝角三角形，将△ABC绕点A按逆时针方向旋转120°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（　　）

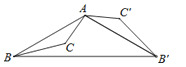A、45° B、60° C、70° D、90°

查看试题解析
6. 关于x的方程x²+2x﹣m＝0有两个相等的实数根，则m的值是（）

A、m＝1 B、m＝﹣1 C、m＝2 D、m＝﹣2

查看试题解析
7. 抛物线y＝x²﹣x+m与x轴至少有一个公共点，则m的取值范围是（）

A、m $\geq \frac{1}{4}$ B、m＞ $\frac{1}{4}$ C、m≤ $\frac{1}{4}$ D、m＜ $\frac{1}{4}$

查看试题解析
8. 如图，将线段AB绕点P按顺时针方向旋转90°，得到线段A'B'，其中点A，B的对应点分别是点A'，B'，则点A'的坐标是（）

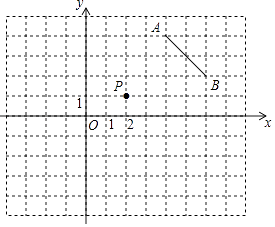A、（﹣1，3） B、（4，0） C、（3，﹣3） D、（5，﹣1）

查看试题解析
9. 如图，在△ABC中，∠CAB＝70°，∠B＝30°，在同一平面内，将△ABC绕点A逆时针旋转40°到△A′B′C′的位置，则∠CC′B′＝（）

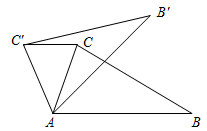A、10° B、15° C、20° D、30°

查看试题解析
10. 如图，抛物线y＝ax²+bx+c的对称轴为x＝﹣1，且过点（ $\frac{1}{2}$ ，0），有下列结论：①abc＞0； ②a﹣2b+4c＞0；③25a﹣10b+4c＝0；④3b+2c＞0；其中所有正确的结论是（）

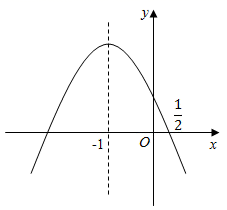A、①③ B、①③④ C、①②③ D、①②③④

查看试题解析

二、填空题。

11. 一元二次方程 ${2x}^{2} - 3x + 1 = 0$ 的解为.

查看试题解析
12. 抛物线y＝2x²﹣4x+8的对称轴是.

查看试题解析
13. 点P（﹣2，4）关于原点的对称点的坐标是.

查看试题解析
14. 一元二次方程x²﹣4x+4=0的解是．

查看试题解析
15. 二次函数y＝x²﹣4x+m的最小值是2，则m＝.

查看试题解析
16. 关于x的方程x²﹣m²x+3m＝0的两个实数根的和为4，则m的值是.

查看试题解析
17. 已知a是方程x²+3x+1＝0的根，则 $\frac{2019 a}{a^{2} + 1}$ ＝.

查看试题解析
18. 将A（2，0）绕原点顺时针旋转40°，A旋转后的对应点是A₁ ，再将A₁绕原点顺时针旋转40°，A₁旋转后的对应点是A₂ ，再将A₂绕原点顺时针旋转40°，A₂旋转后的对应点是A₃ ，再将A₃绕原点顺时针旋转40°，A₃旋转后的对应点是A₄…，按此规律继续下去，A₂₀₁₉的坐标是.

查看试题解析

三、解答题。

19. 如图，△ABC三个顶点的坐标分别是A（﹣2，2），B（﹣3，2），C（﹣1，1）.

(1)、①将△ABC向右平移4个单位得△A₁B₁C₁ ，画出△A₁B₁C₁；
②画出△A₁B₁C₁关于原点对称的△A₂B₂C₂；

(2)、由△ABC和△A₂B₂C₂组成的图形是中心对称图形吗？如果是，请直接写出对称中心的坐标.

查看试题解析
20. 解方程

(1)、2x²﹣4x﹣1＝0（配方法）.

(2)、3x²﹣4x﹣4＝0（公式法）.

查看试题解析
21. 如图，抛物线y＝x²﹣2x﹣3与x轴交于A，B两点，与y轴交于点D，抛物线的顶点为C.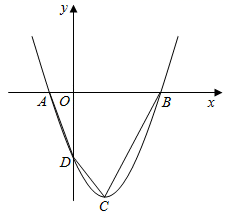

(1)、求A，B，C，D的坐标；

(2)、求四边形ABCD的面积.

查看试题解析
22. 汽车产业的发展，有效促进了我国现代化建设.某汽车销售公司2016年盈利1000万元，2018年盈利1440万元，且从2016年到2018年，每年盈利的年增长率相同.

(1)、求每年盈利的年增长率；

(2)、若该公司盈利的年增长率继续保持不变，预计2019年盈利多少万元？

查看试题解析
23. 如图，ABCD是一个矩形菜园，为了节省材料，使AD边靠墙，其它三边用总长为200m的竹篱笆围成，墙的长度为90m.

(1)、若菜园的面积为4800m² ，求BC边长；

(2)、BC边长为多少时，围成的菜园面积最大？最大值是多少？

查看试题解析
24. 某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件.后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件.

(1)、求商场经营该商品原来一天可获利润多少元？

(2)、设后来该商品每件降价x元，商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？

②求出y与x之间的函数关系式，并直接写出当x取何值时，商场可获得最大利润，最大利润为多少元？

查看试题解析
25. 如图①，△ABC和△BDF均为等腰直角三角形，∠ACB＝∠BDF＝90°，点D在AB上，以CA，CD为邻边作平行四边形CAED，连接EA，EF.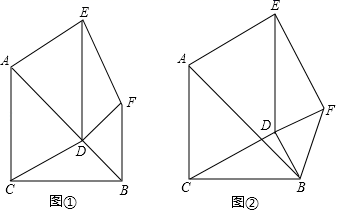

(1)、求证：EA＝EF且EA⊥EF；

(2)、将图①中△BDF绕点B顺时针旋转，其它条件不变，（1）的结论是否成立？请结合图②说明理由.

(3)、若BC＝3，BD＝ $\sqrt{2}$ ，将图①中△BDF绕点B顺时针旋转180°，直接写出AF的最大值和最小值.

查看试题解析
26. 如图，抛物线y＝ax²+bx+2经过A（﹣1，0），B（2，0）两点，与y轴交于点C.

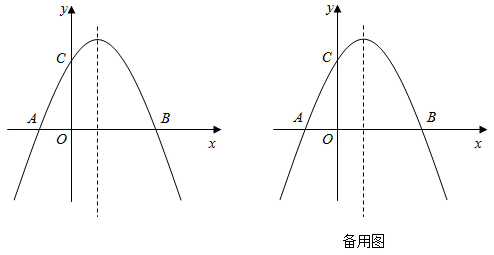(1)、求抛物线的解析式；

(2)、M在抛物线上，线段MA绕点M顺时针旋转90°得MD，当点D在抛物线的对称轴上时，求点M的坐标；

(3)、P在对称轴上，Q在抛物线上，以P，Q，B，C为顶点的四边形为平行四边形，直接写出点P的坐标.

查看试题解析