西藏2020年中考数学试卷
试卷更新日期:2020-09-07 类型:中考真卷
一、选择题
-
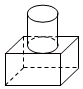
1. 20+(﹣20)的结果是( )A、 ﹣40 B、0 C、20 D、402. 如图,一个由圆柱和长方体组成的几何体水平放置,它的俯视图是( )
 A、
A、 B、
B、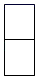 C、
C、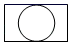 D、
D、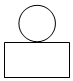 3. 今年以来,西藏自治区劳动就业服务局积极落实失业保险稳岗返还政策,在相关部门的配合与大力帮助下,兑现稳岗返还资金16000000元,将16000000用科学记数法表示为( )A、16×106 B、1.6×107 C、1.6×108 D、0.16×1084. 下列分解因式正确的一项是( )A、x2﹣9=(x+3)(x﹣3) B、2xy+4x=2(xy+2x) C、x2﹣2x﹣1=(x﹣1)2 D、x2+y2=(x+y)25. 一个多边形的内角和是外角和的4倍,则这个多边形的边数是( )A、8 B、9 C、10 D、116. 下列运算正确的是( )A、2a•5a=10a B、(-a3)2+(-a2)3=a5 C、(-2a)3=-6a3 D、a6÷a2=a4(a≠0)7. 如图,下列四个条件中,能判定平行四边形ABCD为菱形的是( )
3. 今年以来,西藏自治区劳动就业服务局积极落实失业保险稳岗返还政策,在相关部门的配合与大力帮助下,兑现稳岗返还资金16000000元,将16000000用科学记数法表示为( )A、16×106 B、1.6×107 C、1.6×108 D、0.16×1084. 下列分解因式正确的一项是( )A、x2﹣9=(x+3)(x﹣3) B、2xy+4x=2(xy+2x) C、x2﹣2x﹣1=(x﹣1)2 D、x2+y2=(x+y)25. 一个多边形的内角和是外角和的4倍,则这个多边形的边数是( )A、8 B、9 C、10 D、116. 下列运算正确的是( )A、2a•5a=10a B、(-a3)2+(-a2)3=a5 C、(-2a)3=-6a3 D、a6÷a2=a4(a≠0)7. 如图,下列四个条件中,能判定平行四边形ABCD为菱形的是( )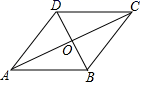 A、∠ADB=90° B、OA=OB C、OA=OC D、AB=BC8. 格桑同学一周的体温监测结果如下表:
A、∠ADB=90° B、OA=OB C、OA=OC D、AB=BC8. 格桑同学一周的体温监测结果如下表:星期
一
二
三
四
五
六
日
体温(单位:℃)
36.6
35.9
36.5
36.2
36.1
36.5
36.3
分析上表中的数据,众数、中位数、平均数分别是( )
A、35.9,36.2,36.3 B、35.9,36.3,36.6 C、36.5,36.3,36.3 D、36.5,36.2,36.69. 如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )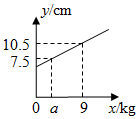 A、3 B、4 C、5 D、610. 如图,AB为半圆O的直径,C为半圆上的一点,OD⊥AC,垂足为D,延长OD与半圆O交于点E.若AB=8,∠CAB=30°,则图中阴影部分的面积为( )
A、3 B、4 C、5 D、610. 如图,AB为半圆O的直径,C为半圆上的一点,OD⊥AC,垂足为D,延长OD与半圆O交于点E.若AB=8,∠CAB=30°,则图中阴影部分的面积为( )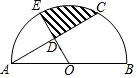 A、 B、 C、 D、11. 如图,在平面直角坐标系中,直线y=x与反比例函数y= (x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A、 B、 C、 D、11. 如图,在平面直角坐标系中,直线y=x与反比例函数y= (x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )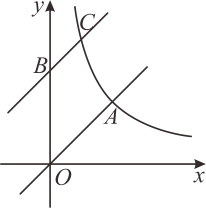 A、1 B、2 C、3 D、412. 观察下列两行数:
A、1 B、2 C、3 D、412. 观察下列两行数:1,3,5,7,9,11,13,15,17,…
1,4,7,10,13,16,19,22,25,…
探究发现:第1个相同的数是1,第2个相同的数是7,…,若第n个相同的数是103,则n等于( )
A、18 B、19 C、20 D、21二、填空题
-
13. 若 在实数范围内有意义,则实数x的取值范围是.14. 分式方程 = 的解为.15. 计算:(π﹣1)0+|﹣2|+ =.16. 如图,已知平行四边形ABCD,以点A为圆心,适当长为半径画弧分别交AB,AD于点E,F,再分别以点E,F为圆心,大于 EF的长为半径画弧,两弧在∠DAB的内部相交于点G,画射线AG交DC于H.若∠B=140°,则∠DHA=.
 17. 当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=.18. 如图,在矩形ABCD中,E为AB的中点,P为BC边上的任意一点,把 沿PE折叠,得到 ,连接CF.若AB=10,BC=12,则CF的最小值为.
17. 当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=.18. 如图,在矩形ABCD中,E为AB的中点,P为BC边上的任意一点,把 沿PE折叠,得到 ,连接CF.若AB=10,BC=12,则CF的最小值为.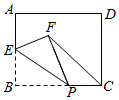
三、解答题
-
19. 解不等式组: 并把解集在数轴上表示出来.
 20. 如图, 中,D为BC边上的一点,AD=AC,以线段AD为边作 ,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.
20. 如图, 中,D为BC边上的一点,AD=AC,以线段AD为边作 ,使得AE=AB,∠BAE=∠CAD.求证:DE=CB.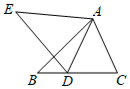 21. 某校组织开展运动会,小明和扎西两名同学准备从100米短跑(记为项目A),800米中长跑(记为项目B),跳远(记为项目C),跳高(记为项目D),即从A,B,C,D四个项目中,分别选择一个项目参加比赛.请用画树状图或列表法求两名同学选到相同项目的概率.22. 如图所示,某建筑物楼顶有信号塔EF,卓玛同学为了探究信号塔EF的高度,从建筑物一层A点沿直线AD出发,到达C点时刚好能看到信号塔的最高点F,测得仰角∠ACF=60°,AC长7米.接着卓玛再从C点出发,继续沿AD方向走了8米后到达B点,此时刚好能看到信号塔的最低点E,测得仰角∠B=30°.(不计卓玛同学的身高)求信号塔EF的高度(结果保留根号).
21. 某校组织开展运动会,小明和扎西两名同学准备从100米短跑(记为项目A),800米中长跑(记为项目B),跳远(记为项目C),跳高(记为项目D),即从A,B,C,D四个项目中,分别选择一个项目参加比赛.请用画树状图或列表法求两名同学选到相同项目的概率.22. 如图所示,某建筑物楼顶有信号塔EF,卓玛同学为了探究信号塔EF的高度,从建筑物一层A点沿直线AD出发,到达C点时刚好能看到信号塔的最高点F,测得仰角∠ACF=60°,AC长7米.接着卓玛再从C点出发,继续沿AD方向走了8米后到达B点,此时刚好能看到信号塔的最低点E,测得仰角∠B=30°.(不计卓玛同学的身高)求信号塔EF的高度(结果保留根号). 23. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
23. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.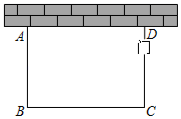 24. 如图所示,AB是⊙O的直径,AD和BC分别切⊙O于A,B两点,CD与⊙O有公共点E,且AD=DE.
24. 如图所示,AB是⊙O的直径,AD和BC分别切⊙O于A,B两点,CD与⊙O有公共点E,且AD=DE.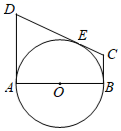 (1)、求证:CD是⊙O的切线;(2)、若AB=12,BC=4,求AD的长.25. 在平面直角坐标系中,二次函数y= x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.
(1)、求证:CD是⊙O的切线;(2)、若AB=12,BC=4,求AD的长.25. 在平面直角坐标系中,二次函数y= x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点. (1)、求二次函数的解析式;(2)、如图甲,连接AC,PA,PC,若 ,求点P的坐标;(3)、如图乙,过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D,交⊙M于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE的长.
(1)、求二次函数的解析式;(2)、如图甲,连接AC,PA,PC,若 ,求点P的坐标;(3)、如图乙,过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D,交⊙M于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE的长.