广东省深圳市罗湖区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 已知x=1是方程x2﹣2x+c=0的一个根,则实数c的值是( )A、﹣1 B、0 C、1 D、22. 如图,是一种氮气弹簧零件的实物图,可以近似看成两个圆柱对接而成,其左视图是( )
 A、
A、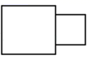 B、
B、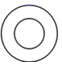 C、
C、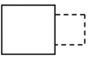 D、
D、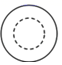 3. 为了估计湖里有多少条鱼,小刚先从湖里捞出了100条鱼做上标记,然后放回湖里去.经过一段时间,带有标记的鱼完全混合于鱼群后,小刚又从湖里捞出200条鱼,如果其中15条有标记,那么估计湖里有鱼( )A、1333条 B、3000条 C、300条 D、1500条4. 下列说法错误的是( )A、高矮不同的两个人在同一盏路灯下同一时刻的影子有可能一样长 B、对角线互相垂直的四边形是菱形 C、方程x2=x的根是x1=0,x2=1 D、对角线相等的平行四边形是矩形5. 受全国生猪产能下降影响,深圳市猪肉价格自5月份开启持续上涨通道,8月份至今创历年新高.某超市8月份价格平均25元/斤,10月份36元/斤,求该超市这两个月猪肉价格平均每月的增长率,设两个月该超市猪肉价格的月平均增长率为x,则可列方程( )A、25(1+x)2=36 B、25(1+2x)=36 C、25(1+x2)=36 D、25+x2=366. 如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2a,则BE长为( )
3. 为了估计湖里有多少条鱼,小刚先从湖里捞出了100条鱼做上标记,然后放回湖里去.经过一段时间,带有标记的鱼完全混合于鱼群后,小刚又从湖里捞出200条鱼,如果其中15条有标记,那么估计湖里有鱼( )A、1333条 B、3000条 C、300条 D、1500条4. 下列说法错误的是( )A、高矮不同的两个人在同一盏路灯下同一时刻的影子有可能一样长 B、对角线互相垂直的四边形是菱形 C、方程x2=x的根是x1=0,x2=1 D、对角线相等的平行四边形是矩形5. 受全国生猪产能下降影响,深圳市猪肉价格自5月份开启持续上涨通道,8月份至今创历年新高.某超市8月份价格平均25元/斤,10月份36元/斤,求该超市这两个月猪肉价格平均每月的增长率,设两个月该超市猪肉价格的月平均增长率为x,则可列方程( )A、25(1+x)2=36 B、25(1+2x)=36 C、25(1+x2)=36 D、25+x2=366. 如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2a,则BE长为( ) A、( +1)a B、( ﹣1)a C、(3﹣ )a D、( ﹣2)a7. 如图, 与 相似,且 ,则下列比例式中正确的是( )
A、( +1)a B、( ﹣1)a C、(3﹣ )a D、( ﹣2)a7. 如图, 与 相似,且 ,则下列比例式中正确的是( )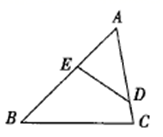 A、 B、 C、 D、8. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )
A、 B、 C、 D、8. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )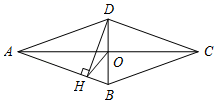 A、120° B、130° C、140° D、150°9. 《代数学》中记载,形如 的方程,求正数解的几何方法是:“如图1,先构造一个面积为 的正方形,再以正方形的边长为一边向外构造四个面积为 的矩形,得到大正方形的面积为 ,则该方程的正数解为 .”小聪按此方法解关于 的方程 时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
A、120° B、130° C、140° D、150°9. 《代数学》中记载,形如 的方程,求正数解的几何方法是:“如图1,先构造一个面积为 的正方形,再以正方形的边长为一边向外构造四个面积为 的矩形,得到大正方形的面积为 ,则该方程的正数解为 .”小聪按此方法解关于 的方程 时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )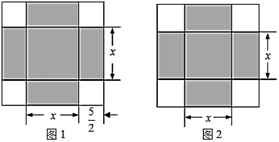 A、6 B、 C、 D、10. 如图,在矩形ABCD中,AB=12,BC=16,将矩形ABCD沿EF折叠,使点B与点D重合,则折痕EF的长为( )
A、6 B、 C、 D、10. 如图,在矩形ABCD中,AB=12,BC=16,将矩形ABCD沿EF折叠,使点B与点D重合,则折痕EF的长为( )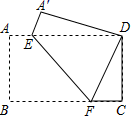 A、14 B、 C、 D、1511. 如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是ts(0<t≤15),过点D作DF⊥BC于点F,连接DE,EF,若四边形AEFD为菱形,则t的值为( )
A、14 B、 C、 D、1511. 如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是ts(0<t≤15),过点D作DF⊥BC于点F,连接DE,EF,若四边形AEFD为菱形,则t的值为( )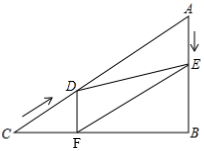 A、20 B、15 C、10 D、512. 如图所示,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AP=EF;③AH⊥EF;④AP2=PM•PH;⑤EF的最小值是 .其中正确结论有( )
A、20 B、15 C、10 D、512. 如图所示,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AP=EF;③AH⊥EF;④AP2=PM•PH;⑤EF的最小值是 .其中正确结论有( )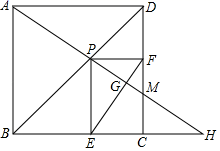 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
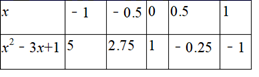
13. 已知 ,若b+d≠0,则 = .14. 已知x2﹣3x+1=0,依据下表,它的一个解的范围是 .
 15. 如图,地面上铺满了正方形的地砖(40cm×40cm),现在向这一地面上抛掷半径为5cm的圆碟,圆碟与地砖间的间隙相交的概率是 .
15. 如图,地面上铺满了正方形的地砖(40cm×40cm),现在向这一地面上抛掷半径为5cm的圆碟,圆碟与地砖间的间隙相交的概率是 . 16. 如图平面直角坐标系中,直线y=kx+1与x轴交于点A点,与y轴交于B点,P(a,b)是这条直线上一点,且a、b(a<b)是方程x2﹣6x+8=0的两根.Q是x轴上一动点,N是坐标平面内一点,以点P、B、Q、N四点为顶点的四边形恰好是矩形,则点N的坐标为或 .
16. 如图平面直角坐标系中,直线y=kx+1与x轴交于点A点,与y轴交于B点,P(a,b)是这条直线上一点,且a、b(a<b)是方程x2﹣6x+8=0的两根.Q是x轴上一动点,N是坐标平面内一点,以点P、B、Q、N四点为顶点的四边形恰好是矩形,则点N的坐标为或 .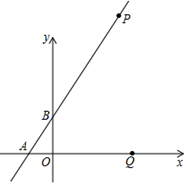
三、解答题
-
17. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.18. 解下列方程(1)、2x2﹣4x﹣3=0(2)、(x﹣1)2=(1﹣x)19. 如图,△ABC在平面直角坐标系中,三个顶点坐标分别为A(0,3)、B(3、4)、C(2,2)(网格中每个正方形的边长是1个单位长度).
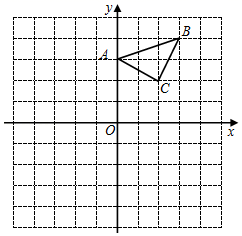 (1)、以点B为位似中心,在网格内画出△A′BC′,使△A′BC′与△ABC位似,且位似比为2:1,则点C′的坐标是;(2)、△A′BC′的面积是平方单位;(3)、在x轴上找出点P,使得点P到B与点A距离之和最小,请直接写出P点的坐标.20. 如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)、以点B为位似中心,在网格内画出△A′BC′,使△A′BC′与△ABC位似,且位似比为2:1,则点C′的坐标是;(2)、△A′BC′的面积是平方单位;(3)、在x轴上找出点P,使得点P到B与点A距离之和最小,请直接写出P点的坐标.20. 如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.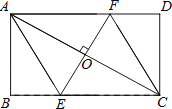 (1)、求证:四边形AECF是菱形;(2)、若AB= ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)21. 如图,在斜坡顶部有一铁塔AB , B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2 m和1 m.已知CD=12 m,DE=18 m,小明和小华身高均为1.6 m,那么塔高AB为多少?
(1)、求证:四边形AECF是菱形;(2)、若AB= ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)21. 如图,在斜坡顶部有一铁塔AB , B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2 m和1 m.已知CD=12 m,DE=18 m,小明和小华身高均为1.6 m,那么塔高AB为多少?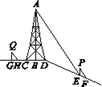 22. 某商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.(1)、若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元?(2)、在(1)的条件下,当该这种书包销售单价为多少元时,销售利润是3120元?(3)、这种书包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.23. 如图,在平面直角坐标系中,过原点O及A(8,0)、C(0,6)作矩形OABC,连接AC,一个直角三角形PDE的直角顶点P始终在对角线AC上运动(不与A、C重合),且保持一边PD始终经过矩形顶点B,PE交x轴于点Q
22. 某商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.(1)、若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元?(2)、在(1)的条件下,当该这种书包销售单价为多少元时,销售利润是3120元?(3)、这种书包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.23. 如图,在平面直角坐标系中,过原点O及A(8,0)、C(0,6)作矩形OABC,连接AC,一个直角三角形PDE的直角顶点P始终在对角线AC上运动(不与A、C重合),且保持一边PD始终经过矩形顶点B,PE交x轴于点Q (1)、 =;(2)、在点P从点C运动到点A的过程中, 的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;(3)、若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为 .
(1)、 =;(2)、在点P从点C运动到点A的过程中, 的值是否发生变化?如果变化,请求出其变化范围,如果不变,请说明理由,并求出其值;(3)、若将△QAB沿直线BQ折叠后,点A与点P重合,则PC的长为 .