广东省深圳市龙岗区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 如图,是由三个相同的小正方体组成的几何体,它的俯视图是( )
 A、
A、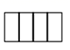 B、
B、 C、
C、 D、
D、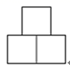 2. 方程 的解是( )A、 , B、 C、 D、 ,3. 若 ,则 的值是( )A、 B、 C、 D、4. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的概率是0.2,则估计盒子中大约有红球( )A、12个 B、16个 C、20个 D、25个5. 给出下列命题:
2. 方程 的解是( )A、 , B、 C、 D、 ,3. 若 ,则 的值是( )A、 B、 C、 D、4. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的概率是0.2,则估计盒子中大约有红球( )A、12个 B、16个 C、20个 D、25个5. 给出下列命题:①对角线相等且互相平分的四边形是矩形;②对角线平分一组对角的平行四边形是菱形;③对角线互相垂直的矩形是正方形;④对角线相等的菱形是正方形;其中是真命题的有( )个.
A、1个 B、2个 C、3个 D、4个6. 若关于x的方程kx2﹣6x+9=0有实数根,则k的取值范围是( )A、k<1 B、k≤1 C、k<1且k≠0 D、k≤1且k≠07. 已知点C是线段AB的黄金分割点(AC<BC),AB=4,则线段AC的长是( )A、 B、 C、 D、8. 书架上放着三本古典名著和两本外国小说,小明从中随机抽取两本,两本都是古典名著的概率是( )A、 B、 C、 D、9. 如图,∠1=∠2,则下列各式不能说明△ABC∽△ADE的是( )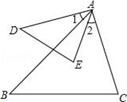 A、∠D=∠B B、∠E=∠C C、 D、10. 一天晚上,小颖由路灯A下的B处向正东走到C处时,测得影子CD的长为1米.当她继续向正东走到D处时,测得此时影子DE的一端E到路灯A的仰角为45°.已知小颖的身高为1.5米,那么路灯AB的高度是多少米?( )
A、∠D=∠B B、∠E=∠C C、 D、10. 一天晚上,小颖由路灯A下的B处向正东走到C处时,测得影子CD的长为1米.当她继续向正东走到D处时,测得此时影子DE的一端E到路灯A的仰角为45°.已知小颖的身高为1.5米,那么路灯AB的高度是多少米?( )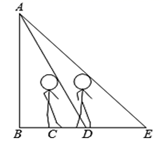 A、4米 B、4.5米 C、5米 D、6米11. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是
A、4米 B、4.5米 C、5米 D、6米11. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 A、 B、 C、5 D、612. 如图,在▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( )
A、 B、 C、5 D、612. 如图,在▱ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( )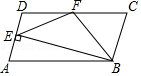 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
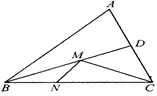
13. 已知菱形的周长为24,较大的内角为120°,则菱形的较长的对角线长为 .14. 已知 是关于x的一元二次方程 (c为常数)的一个根,则方程的另一个根是 .15. 在平面直角坐标系中,矩形 的顶点坐标分别是 , , , , , , , ,已知矩形 与矩形 位似,位似中心为坐标原点 ,位似比为 ,则点 的坐标是 .16. 在锐角三角形ABC中.BC= ,∠ABC=45°,BD平分∠ABC . 若M , N分别是边BD , BC上的动点,则CM+MN的最小值是 .
三、解答题
-
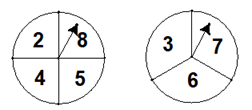
17. 计算:18. 解方程:(1)、 ;(2)、 .19. 如图,两个转盘分别被分成四等分和三等分,并标有数字。旋转停止时,每个转盘上的箭头各指向一个数字,通过树状图或列表法求这两个数字之和为偶数的概率.
 20. 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
20. 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,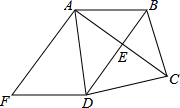 (1)、证明ABDF是平行四边形;(2)、若AF=DF=5,AD=6,求AC的长.21. 某农业合作社投资64000元共收获80吨的农产品,目前,该农产品可以以1200元/吨售出,如果储藏起来,每星期会损失2吨,且每星期需支付各种费用1600元,且同时每星期每吨价格将上涨200元.问储藏多少星期出售这批农产品可获利122000元?22. 如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.
(1)、证明ABDF是平行四边形;(2)、若AF=DF=5,AD=6,求AC的长.21. 某农业合作社投资64000元共收获80吨的农产品,目前,该农产品可以以1200元/吨售出,如果储藏起来,每星期会损失2吨,且每星期需支付各种费用1600元,且同时每星期每吨价格将上涨200元.问储藏多少星期出售这批农产品可获利122000元?22. 如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD折叠,点C落在点C′的位置,BC′交AD于点G.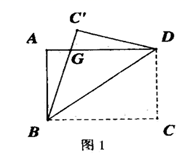
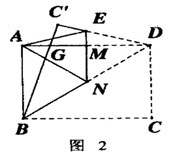 (1)、求证:BG=DG;(2)、求C′G的长;(3)、如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.23. 已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3 cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为 cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
(1)、求证:BG=DG;(2)、求C′G的长;(3)、如图2,再折叠一次,使点D与A重合,折痕EN交AD于M,求EM的长.23. 已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3 cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为 cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题: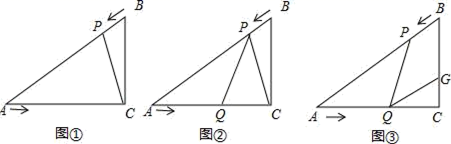 (1)、如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;(2)、如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;(3)、如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.
(1)、如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;(2)、如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;(3)、如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.