广东省茂名市高州市2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-07 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列说法中，错误的是（   ）
    A、菱形的对角线互相垂直平分 B、正方形的对角线互相垂直平分且相等 C、矩形的对角线相等且平分 D、平行四边形的对角线相等且垂直

    查看试题解析

  • 2. 用公式法解﹣x2+3x＝1时，先求出a、b、c的值，则a、b、c依次为（ ）
    A、﹣1，3，1 B、1，3，1 C、﹣1，3，﹣1 D、1，﹣3，﹣1

    查看试题解析

  • 3. 小新抛一枚质地均匀的硬币，连续抛三次，硬币落地均正面朝上，如果他第四次抛硬币，那么硬币正面朝上的概率为（   ）

    A、12 B、14 C、1 D、34

    查看试题解析

  • 4. 若a ， b ， c ， d是成比例线段，其中a＝3cm ， c＝6cm ， d＝4cm ， 则b等于（   ）
    A、8 cm B、32 cm C、4 cm D、2cm

    查看试题解析

  • 5. 菱形的边长是2cm，一条对角线的长是2cm，则另一条对角线的长约是（   ）
    A、4cm B、1cm C、3 cm D、23 cm

    查看试题解析

  • 6. 用配方法解一元二次方程x2+6x﹣3＝0，原方程可变形为（   ）
    A、（x+3）2＝9 B、（x+3）2＝12 C、（x+3）2＝15 D、（x+3）2＝39

    查看试题解析

  • 7. 如图所示，小明、小刚利用两个转盘进行游戏，规则为小明将两个转盘各转一次，如配成紫色（红与蓝），小明胜，否则小刚胜，此规则（   ）

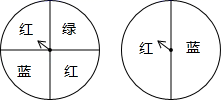    A、公平 B、对小明有利 C、对小刚有利 D、公平性不可预测

    查看试题解析

  • 8.

    如图，在△ABC中，DE∥BC，AD=6，DB=3，AE=4，则EC的长为（　　）

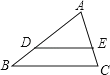    A、1 B、2 C、3 D、4

    查看试题解析

  • 9. 如图，在一幅矩形风景画外面的四周镶一条金色纸边，制成一幅矩形挂图，整个挂图的长80cm ， 宽50cm如图所示，如果风景画的面积是3500cm2 ． 设金色纸边的宽为xcm ， 那么x满足的方程是（   ）

    A、（80﹣x）（50﹣x）＝3500 B、（80﹣2x）（50﹣2x）＝3500 C、（80+x）（50+x）＝3500 D、（80+2x）（50+2x）＝3500

    查看试题解析

  • 10. 已知a4=b5=c6 ， 且a-b+c=10，则a+b-c的值为（　　）

    A、6 B、5 C、4 D、3

    查看试题解析

二、填空题

  • 11. 如图，在平行四边形ABCD中，添加一个条件使平行四边形ABCD是菱形。

    查看试题解析

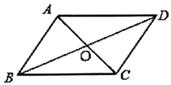  • 12. 方程 ax2+bx+c=0(a≠0) 的判别式是 ， 求根公式是 ．

    查看试题解析

  • 13. 一个不透明的袋子中装有黑、白小球各两个，这些小球除颜色外无其他差别，从袋子中随机摸出一个小球后，放回并摇匀，再随机摸出一个小球，则两次摸出的小球都是白球的概率为 ．

    查看试题解析

  • 14. 已知线段AB的长为10米，P是AB的黄金分割点（AP＞BP），则AP的长米．（精确到0.01米）

    查看试题解析

  • 15. 王老师假期中去参加高中同学聚会，聚会时，所有到会的同学都互相握了一次手，王老师发现共握手435次，则参加聚会的同学共有多少人?设参加聚会的同学共有x人，则根据题意，可列方程。

    查看试题解析

  • 16. 如图，P、G是菱形ABCD的边BC、DC的中点，K是菱形的对角线BD上的动点，若BD＝8，AC＝6，则KP+KG的最小值是 ．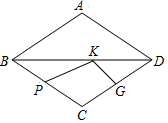

    查看试题解析

三、解答题

  • 17. 如图，在菱形ABCD中，CE＝CF.求证：AE＝AF.

    查看试题解析

  • 18. 解方程：
    (1)、4x（2x+1）＝3（2x+1）
    (2)、2x2+6x﹣3＝0

    查看试题解析

  • 19. 如图，点D在△ABC的AB边上，且∠ACD=∠A．

    (1)、作△BDC的平分线DE，交BC于点E（用尺规作图法，保留作图痕迹，不要求写作法）；
    (2)、在（1）的条件下，判断直线DE与直线AC的位置关系（不要求证明）.

    查看试题解析

  • 20. 已知x＝1是关于x的一元二次方程x2+3x﹣m＝0的一个根，求m的值和方程的另一个根．

    查看试题解析

  • 21. 如图：在平行四边形ABCD中，E是AB延长线上点，DE交BC于点F

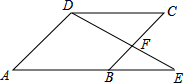    (1)、求证：△DFC∽△EFB；
    (2)、若DC＝6，BE＝4，DE＝10，求DF的长度？

    查看试题解析

  • 22. 商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．
    (1)、若他去买一瓶饮料，则他买到奶汁的概率是；
    (2)、若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶油的概率．

    查看试题解析

  • 23. 已知：如图，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交于点F ， 连接AE ， CF ．

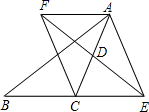    (1)、求证：AF＝CE；
    (2)、若AC＝EF ， 试判断四边形AFCE是什么样的四边形，并证明你的结论．

    查看试题解析

  • 24. 某商场销售一批名牌衬衫，平均每天可销售20件，每件盈利40元。为了扩大销售增加盈利，尽量减少库存，商场决定采取适当的降价措施。经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。
    (1)、若商场每件降价4元，问商场每天可盈利多少元。
    (2)、若商场平均每天要盈利1200元，且让顾客尽可能多得实惠每件衬衫应降价多少元。
    (3)、要使商场平均每天盈利1600元，可能吗?请说明理由。

    查看试题解析

  • 25. 如图，在正方形ABCD中，E为边AD上的点，点F在边CD上，且CF＝3FD ， ∠BEF＝90°

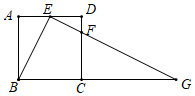    (1)、求证：△ABE∽△DEF；
    (2)、若AB＝4，延长EF交BC的延长线于点G ， 求BG的长

    查看试题解析