安徽省淮北市2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 在比例尺是1:4000的安庆市城区地图上,菱湖南路的长度约为 ,它的实际长度约为( )A、160cm B、160m C、1000cm D、1000m2. 二次函数 图像的顶点坐标是( )A、 B、 C、 D、3. 如图,已知 , , , 的长为( )
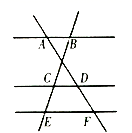 A、2 B、4 C、3 D、54. 如图, , 相交于点 ,过点 的直线分别交 于点 ,则下列结论不一定成立的是( )
A、2 B、4 C、3 D、54. 如图, , 相交于点 ,过点 的直线分别交 于点 ,则下列结论不一定成立的是( )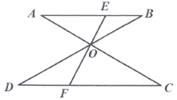 A、 B、 C、 D、5. 已知点 在反比例函数 的图像上,若 ,则 、0的大小关系为( )A、 B、 C、 D、6. 共享单车为市民出行带来了方便,某单车公式第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )A、y=a(1+x)2 B、y=a(1﹣x)2 C、y=(1﹣x)2+a D、y=x2+a7. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是 ,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为 ,则其升高可能是( )
A、 B、 C、 D、5. 已知点 在反比例函数 的图像上,若 ,则 、0的大小关系为( )A、 B、 C、 D、6. 共享单车为市民出行带来了方便,某单车公式第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是( )A、y=a(1+x)2 B、y=a(1﹣x)2 C、y=(1﹣x)2+a D、y=x2+a7. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是 ,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为 ,则其升高可能是( ) A、 B、 C、 D、8. 如图,直线 , , ,则 的值为( )
A、 B、 C、 D、8. 如图,直线 , , ,则 的值为( ) A、2:1 B、1:2 C、2:3 D、3:29. 已知双曲线 的图象如图所示,则函数 与 的图象大致是( )
A、2:1 B、1:2 C、2:3 D、3:29. 已知双曲线 的图象如图所示,则函数 与 的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )
10. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( )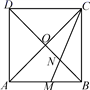 A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
11. 如图,在 中,点 为 上一点,连接 .若再添加一个条件,使 ,则需添加的一个条件是.
 12. 将抛物线 向左平移2个单位,再向上平移2个单位后,得到新抛物线的解析式为.13. 如图, , 分别是 边 , 上的点, ,若 , , ,则 .
12. 将抛物线 向左平移2个单位,再向上平移2个单位后,得到新抛物线的解析式为.13. 如图, , 分别是 边 , 上的点, ,若 , , ,则 . 14. 当 时,反比例函数 ( 且 )的最大值与最小值之差是1,则 的值是.
14. 当 时,反比例函数 ( 且 )的最大值与最小值之差是1,则 的值是.三、解答题
-
15. 已知 ,求代数式 的值.16. 已知二次函数 的图像经过点 和点 ,求该函数的表达式,并求出当 时, 的最值.17. 如图,在平面直角坐标系中,每个小正方形的边长都是1个单位长度, 的顶点都在格点上.
 (1)、以原点 为位似中心,在第三象限内画出将 放大为原来的2倍后的位似图形 ;(2)、已知 的面积为4,则 的面积是.18. 如图,已知抛物线 与 轴相交于点 , (点 在点 的左侧),与 轴相交于点 ,直线 经过点 , .
(1)、以原点 为位似中心,在第三象限内画出将 放大为原来的2倍后的位似图形 ;(2)、已知 的面积为4,则 的面积是.18. 如图,已知抛物线 与 轴相交于点 , (点 在点 的左侧),与 轴相交于点 ,直线 经过点 , . (1)、求直线 的函数关系式;(2)、当 时,请直接写出 的取值范围.19. 如图,在正方形 中, ,点 在 轴的负半轴上,点 在 轴的正半轴上,点 在边 上,且 交 于点 ,反比例函数 的图像经过点 .若 ,求 的值.
(1)、求直线 的函数关系式;(2)、当 时,请直接写出 的取值范围.19. 如图,在正方形 中, ,点 在 轴的负半轴上,点 在 轴的正半轴上,点 在边 上,且 交 于点 ,反比例函数 的图像经过点 .若 ,求 的值. 20. 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
20. 如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.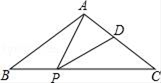 (1)、求证:△ABP∽△PCD;(2)、若AB=10,BC=12,当PD∥AB时,求BP的长.21. 如图,已知双曲线 ,经过点 .
(1)、求证:△ABP∽△PCD;(2)、若AB=10,BC=12,当PD∥AB时,求BP的长.21. 如图,已知双曲线 ,经过点 . (1)、求 的值;(2)、过 作 轴,垂足为 ,点 是双曲线的一点,连接 , ,若 的面积为12,求直线 的解析式.22. 如图,在矩形 中,点 是 的中点, 于点 .
(1)、求 的值;(2)、过 作 轴,垂足为 ,点 是双曲线的一点,连接 , ,若 的面积为12,求直线 的解析式.22. 如图,在矩形 中,点 是 的中点, 于点 . (1)、若 ,求 的长;(2)、在(1)的条件下,连接 ,求 的长.23. 某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
(1)、若 ,求 的长;(2)、在(1)的条件下,连接 ,求 的长.23. 某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:售价x(元/千克)
40
39
38
37
销售量y(千克)
20
22
24
26
(1)、求y与x之间的函数表达式;(2)、设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?(3)、该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?