安徽省合肥市瑶海区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，y是的二次函数的是（）

A、 $y = \frac{1}{x}$ B、 $y = - 2 x + 1$ C、 $y = x^{2} - 2$ D、 $y = 3 x$

查看试题解析
2. 已知3x=5y（y≠0），则下列比例式成立的是（）

A、 $\frac{x}{3} = \frac{5}{y}$ B、 $\frac{x}{5} = \frac{y}{3}$ C、 $\frac{x}{y} = \frac{3}{5}$ D、 $\frac{x}{3} = \frac{y}{5}$

查看试题解析
3. 抛物线y＝x²+1经过平移得到抛物线y＝（x+1）² ，平移的方法是（）

A、向左平移1个，再向下平移1个单位 B、向右平移1个，再向下平移1个单位 C、向左平移1个，再向上平移1个单位 D、向右平移1个，再向上平移1个单位

查看试题解析
4. 如图，在△ABC中，DE∥BC，AD＝6，DB＝3，AE＝4，则AC的长为（）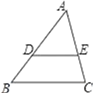

A、2 B、4 C、6 D、8

查看试题解析
5. 点C是线段AB的黄金分割点（AC＜CB），若AC＝2，则CB＝（）

A、 $\sqrt{5}$ +1 B、 $\sqrt{5}$ +3 C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\frac{3 - \sqrt{5}}{2}$

查看试题解析
6. 如图所示是二次函数y=ax²﹣x+a²﹣1的图象，则a的值是（）

A、a=﹣1 B、a= $\frac{1}{2}$ C、a=1 D、a=1或a=﹣1

查看试题解析

7. 二次函数y＝ax²+bx+c的自变量x与函数值y的对应值如图，下列说法错误的是：（）

x	…	﹣6	﹣5	﹣4	﹣3	﹣2	﹣1	…
y	…	10	4	0	﹣2	﹣2	0	…

A、抛物线开口向上 B、抛物线与y轴的交点是（0，4） C、当x＜﹣2时，y随x的增大而减小 D、当x＞﹣2时，y随x的增大而增大

查看试题解析

8. 某企业是一家专门生产季节性产品的企业，当产品无利润时，企业会自动停产，经过调研预测，它一年中每月获得的利润 $y ($ 万元 $)$ 和月份n之间满足函数关系式 $y = - n^{2} + 14 n - 24$ ，则企业停产的月份为（）

A、2月和12月 B、2月至12月 C、1月 D、1月、2月和12月

查看试题解析
9. 已知函数y＝ax²+bx+c的图象如图所示，则关于x的方程ax²+bx+c﹣4＝0的根的情况是（）

A、有两个相等的实数根 B、有两个异号的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
10. 已知，二次函数y＝ax²+bx+c满足以下三个条件：① $\frac{b^{2}}{a}$ ＞4c，②a﹣b+c＜0，③b＜c，则它的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若线段a=3 cm,b=12 cm，则a、b的比例中项c=cm．

查看试题解析
12. 在某市中考体考前，某初三学生对自己某次实心球训练的录像进行分析，发现实心球飞行高度y（米）与水平距离x（米）之间的关系为 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，由此可知该生此次实心球训练的成绩为米．

查看试题解析
13. 如图，矩形ABCD的顶点C，D分别在反比例函数y＝ $\frac{8}{x}$ （x＞0）．y＝ $\frac{3}{x}$ （x＞0）的图象上，顶点A，B在x轴上，连接OC，交DA于点E，则 $\frac{OE}{E C}$ ＝．

查看试题解析
14. 已知函数y＝kx²+2kx+1，当﹣3≤x≤2时，函数有最大值为4，则k＝．

查看试题解析

三、解答题

15. 若 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4}$ ≠0，求代数式 $\frac{x + y - z}{x + y + z}$ 的值．

查看试题解析
16. 已知二次函数y＝ax²+bx+c的图象经过（0，3），（﹣1，0），（3，0）三点．

(1)、求二次函数解析式；

(2)、试说明y随x的变化情况．

查看试题解析
17. 已知 $Δ A B C$ 和 $Δ D E F$ 中，有 $\frac{A B}{D E} = \frac{B C}{E F} = \frac{C A}{F D} = \frac{2}{3}$ ,且 $Δ A B C$ 和 $Δ D E F$ 的周长之差为15厘米，求 $Δ A B C$ 和 $Δ D E F$ 的周长.

查看试题解析
18. 如图，菱形ABCD的边长为1，直线l过点C，交AB的延长线于M，交AD的延长线于N，求 $\frac{1}{A M} + \frac{1}{A N}$ 的值．

查看试题解析
19. 直线y＝mx（m为常数）与双曲线y＝ $\frac{k}{x}$ （k为常数）相交于A、B两点．

(1)、若点A的横坐标为3，点B的纵坐标为﹣4．直接写出：k＝， m＝， mx＞ $\frac{k}{x}$ 的解集为．

(2)、若双曲线y＝ $\frac{k}{x}$ （k为常数）的图象上有点C（x₁ ， y₁），D（x₂ ， y₂），当x₁＜x₂时，比较y₁与y₂的大小．

查看试题解析
20. 在平面直角坐标系中，A（0，4）、B（4，4）、C（4，0），D（1，0）．

(1)、若抛物线经过A、B、D三点，求此抛物线的解析式；

(2)、若（1）中的抛物线的顶点为E，连接EB，若P是EB上一动点，过P点作PM⊥AB，PN垂直于y轴，垂足分别是M、N．求矩形AMPN面积的最大值．

查看试题解析
21. 如图所示，双曲线y＝ $\frac{k}{x}$ （x＞0，k＞0）与直线y＝ax+b（a≠0，b为常数）交于A（2，4），B（m，2）两点．

(1)、求m的值；

(2)、若C点坐标为（n，0），当AC+BC的值最小时，求出n的值；

(3)、求△AOB的面积．

查看试题解析
22. 某网店经市场调查，发现进价为40元的某新型文具每月的销售量y（件）与售价x（元）的相关信息如下：

售价x（元）

60

70

80

90

…

销售量y（件）

280

260

240

220

…

(1)、试用你学过的函数来描述y与x的关系，这个函数可以是（填“一次函数”、“反比例函数”或“二次函数”），并求这个函数关系式；

(2)、当售价为多少元时，当月的销售利润最大，最大利润是多少；

(3)、若获利不得高于进价的80%，那么售价定为多少元时，月销售利润达到最大，最大利润是多少？

查看试题解析
23. 定义：在平面直角坐标系中，图形G上点P（x，y）的纵坐标y与其横坐标x的差y﹣x称为点P的“坐标差”，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”．

(1)、求点A（2，1）的“坐标差”和抛物线y＝﹣x²+3x+4的“特征值”．

(2)、某二次函数＝﹣x²+bx+c（c≠0）的“特征值”为﹣1，点B与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等，求此二次函数的解析式．

(3)、如图所示，二次函数y＝﹣x²+px+q的图象顶点在“坐标差”为2的一次函数的图象上，四边形DEFO是矩形，点E的坐标为（7，3），点O为坐标原点，点D在x轴上，当二次函数y＝﹣x²+px+q的图象与矩形的边有四个交点时，求p的取值范围．

查看试题解析

售价x（元）	60	70	80	90	…
销售量y（件）	280	260	240	220	…