安徽省合肥市包河区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 二次函数 的对称轴是A、直线 B、直线 C、y轴 D、x轴2. 若= , 则的值为( )A、1 B、 C、 D、3. 已知二次函数y=(x-1)2-3,则此二次函数( )A、有最大值1 B、有最小值1 C、有最大值-3 D、有最小值-34. 将抛物线 向右平移2个单位,再向下平移1个单位,则平移后抛物线的顶点坐标是( )A、(2,1) B、(2,-1) C、(-2,-1) D、(-2,1)5. 如图,线段 相交于点 .若 ,则 的长为( )
 A、3 B、3.2 C、3.6 D、46. 如图,点P在反比例函数 的图象上,PA⊥x轴于点A , 则△PAO的面积为( )
A、3 B、3.2 C、3.6 D、46. 如图,点P在反比例函数 的图象上,PA⊥x轴于点A , 则△PAO的面积为( ) A、1 B、2 C、4 D、67. 如图,在平面直角坐标系中有 两点,如果抛物线 与线段 有公共点,那么 的取值范围是( )
A、1 B、2 C、4 D、67. 如图,在平面直角坐标系中有 两点,如果抛物线 与线段 有公共点,那么 的取值范围是( ) A、 B、 C、 D、8. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A、 B、 C、 D、8. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )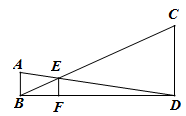 A、 B、 C、 D、9. 心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(单位:min)之间近似满足函数关系s=at2+bt+c(a≠0),s值越大,表示接受能力越强.如图记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为( )
A、 B、 C、 D、9. 心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(单位:min)之间近似满足函数关系s=at2+bt+c(a≠0),s值越大,表示接受能力越强.如图记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为( ) A、8min B、13min C、20min D、25min10. 在平面直角坐标系中,点 的坐标 ,点 的坐标为 为实数),当 长取得最小值时, 的值为( )A、 B、 C、3 D、4
A、8min B、13min C、20min D、25min10. 在平面直角坐标系中,点 的坐标 ,点 的坐标为 为实数),当 长取得最小值时, 的值为( )A、 B、 C、3 D、4二、填空题
-
11. 如图,在 中, ,若 ,则 .
 12. 某水果店销售一批水果,平均每天可售出 ,每千克盈利4元,经调查发现,每千克降价0.5元,商店平均每天可多售出 水果,则商店平均每天的最高利润为元13. 如图,在 轴上方,平行于 轴的直线与反比例函数 和 的图象分别交于 两点,连接 .若 的面积为 则 .
12. 某水果店销售一批水果,平均每天可售出 ,每千克盈利4元,经调查发现,每千克降价0.5元,商店平均每天可多售出 水果,则商店平均每天的最高利润为元13. 如图,在 轴上方,平行于 轴的直线与反比例函数 和 的图象分别交于 两点,连接 .若 的面积为 则 . 14. 已知二次函数 为常数),当 时,y的最大值是15,则m的值是 .15. 已知 ,则 = .
14. 已知二次函数 为常数),当 时,y的最大值是15,则m的值是 .15. 已知 ,则 = .三、解答题
-
16. 抛物线 的顶点为 ,它的形状与 相同,但开口方向与之相反.(1)、直接写出抛物线的解析式;(2)、求抛物线与 轴的交点坐标.17. 如图,正方形 对角线的交点在平面直角坐标系的原点,且边与坐标轴平行或垂直,AB=4.
 (1)、如果反比例函数 的图象经过点 ,求这个反比例函数的表达式;(2)、如果反比例函数 的图象与正方形 有公共点,请直接写出 的取值范围.18. 如图,在 中, 分别是边 上的点,连接 ,且 , .
(1)、如果反比例函数 的图象经过点 ,求这个反比例函数的表达式;(2)、如果反比例函数 的图象与正方形 有公共点,请直接写出 的取值范围.18. 如图,在 中, 分别是边 上的点,连接 ,且 , .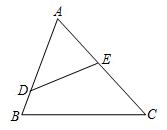 (1)、求证: ;(2)、如果E是AC的中点, 求 的长,19. 已知 中,边 及 边上的高 的和为 .(1)、请直接写出 的面积 与边 的长 之间的函数关系式(不要求写出自变量 的取值范围);(2)、当 是多少时,这个三角形面积 最大?最大面积是多少?20. 一次函数 的图像与双曲线 相交于 和 两点,与 轴相交于点 ,过点 作 轴,垂足为点 .
(1)、求证: ;(2)、如果E是AC的中点, 求 的长,19. 已知 中,边 及 边上的高 的和为 .(1)、请直接写出 的面积 与边 的长 之间的函数关系式(不要求写出自变量 的取值范围);(2)、当 是多少时,这个三角形面积 最大?最大面积是多少?20. 一次函数 的图像与双曲线 相交于 和 两点,与 轴相交于点 ,过点 作 轴,垂足为点 . (1)、求一次函数的解析式;(2)、根据图像直接写出不等式 的解集;(3)、 的面积为
(1)、求一次函数的解析式;(2)、根据图像直接写出不等式 的解集;(3)、 的面积为
21. 如图,在 中, 是 内一点,且 (1)、求 的度数;(2)、求 的面积.
(1)、求 的度数;(2)、求 的面积.

