安徽省滁州市全椒县2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 抛物线y=－2(x－3)²－4的顶点坐标 $($ $)$

A、(－3，4) B、(－3，－4) C、(3，－4) D、(3，4)

查看试题解析
2. 已知 $\frac{x}{y} = \frac{5}{2}$ ，则 $\frac{x - y}{y}$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、 $- \frac{3}{5}$

查看试题解析
3. 若 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ 是函数 $y = \frac{5}{x}$ 图象上的两点，当 $x_{1} > x_{2} > 0$ 时，下列结论正确的是（）

A、 $0 < y_{1} < y_{2}$ B、 $0 < y_{2} < y_{1}$ C、 $y_{1} < y_{2} < 0$ D、 $y_{2} < y_{1} < 0$

查看试题解析
4.
如图，下列条件不能判定△ADB∽△ABC的是（　　）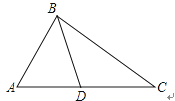

A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB²=AD•AC D、 $\frac{A D}{A B} = \frac{A B}{B C}$

查看试题解析
5. 如图，是三个正方形拼成的一个长方形，则∠1+∠2+∠3=（）

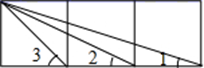A、60° B、75° C、90° D、105°

查看试题解析
6. 如图，图中是抛物线形拱桥，当拱顶离水面2m时水面宽4m．水面下降1m，水面宽度为（）

A、2 $\sqrt{6}$ m B、2 $\sqrt{3}$ m C、 $\sqrt{6}$ m D、 $\sqrt{3}$ m

查看试题解析
7. 如图，在平行四边形ABCD中，E为CD上一点，连接AE ， BD ，且AE ， BD交于点F ， $S_{△ D E F}$ ： $S_{△ B F A} = 9$ ：25，则DE： $E C$ =（）

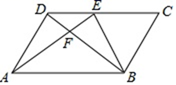A、2：5 B、3：2 C、2：3 D、5：3

查看试题解析
8. 在同一坐标系下，抛物线y₁=﹣x²+4x和直线y₂=2x的图象如图所示，那么不等式﹣x²+4x＞2x的解集是（）

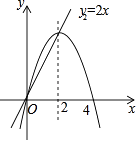A、x＜0 B、0＜x＜2 C、x＞2 D、x＜0或 x＞2

查看试题解析
9. 如图是小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB＝1.2米，BP＝1.8米，PD＝12米，那么该古城墙的高度是（）

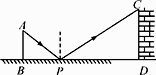A、6米 B、8米 C、18米 D、24米

查看试题解析
10.
如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=3，AD=4，BC=3 $\sqrt{3}$ ，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 如果二次函数y=（m﹣2）x²+3x+m²﹣4的图象经过原点，那么m= ．

查看试题解析
12. 如果点 $P$ 把线段 $A B$ 分割成 $A P$ 和 $P B$ 两段( $A P > P B$ )，其中 $A P$ 是 $A B$ 与 $P B$ 的比例中项，那么 $A P ： A B$ 的值为．

查看试题解析
13. 如图，反比例函数y= $\frac{k}{x}$ 的图象经过▱ABCD对角线的交点P，已知点A，C，D在坐标轴上，BD⊥DC，▱ABCD的面积为6，则k= ．

查看试题解析
14. 在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D、E分别在AC、AB上，且△ADE是直角三角形，△BDE是等腰三角形，则BE=.

查看试题解析

三、解答题

15. 如果 $\frac{x + 3}{2} = \frac{y - 1}{3} = \frac{z - 2}{4}$ ，且x＋y＋z＝18，求x ， y ， z的值．

查看试题解析
16. 已知二次函数的图象以 $A (- 1, 4)$ 为顶点，且过点 $B (2, - 5)$

(1)、求该函数的关系式；

(2)、求该函数图象与坐标轴的交点坐标；

查看试题解析
17. 已知：如图，在△ABC中，D是AC上一点， $\frac{C B}{C D} = \frac{C A}{C B} = \frac{3}{2}$ ，△BCD的周长是24cm ．

(1)、求△ABC的周长；

(2)、求△BCD与△ABD的面积比．

查看试题解析
18. 如图，直立在点 $B$ 处的标杆 $A B$ 长 $2.5 m$ ，站立在点 $F$ 处的观察者从点 $E$ 处看到标杆顶 $A$ 、旗杆顶 $C$ 在一条直线上．已知 $B D = 18 m$ ， $F B = 3 m$ ， $E F = 1.6 m$ ，求旗杆高 $C D$ ．

查看试题解析
19. 一块材料的形状是锐角三角形ABC，边BC=120mm，高4D=80mm， .把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上.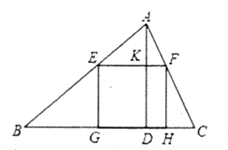

(1)、求证： $Δ A E F ~ Δ A B C$ ；

(2)、求这个正方形零件的边长；

查看试题解析
20. 如图，一次函数 $y = - x + 4$ 的图象与反比例函数 $y = \frac{k}{x}$ ( $k$ 为常数，且 $k \neq 0$ )的图象交于 $A (1 ， a) ， B (3 ， b)$ 两点.

(1)、求反比例函数的表达式；

(2)、在x轴上找一点 $P$ ，使 $P A + P B$ 的值最小，求满足条件的点 $P$ 的坐标；

(3)、在(2)的条件下，求 $△ P A B$ 的面积.

查看试题解析
21. 在Rt△ABC中，∠C＝90°，AC＝20cm，BC＝15cm.现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB也向点B方向运动.如果点P的速度是4cm/秒，点Q的速度是2cm/秒，它们同时出发，当有一点到达所在线段的端点时，就停止运动，设运动的时间为t秒.

(1)、用含t的代数式表示Rt△CPQ的面积S；

(2)、当t＝3秒时，P、Q两点之间的距离是多少？

(3)、当t为多少秒时，以点C、P、Q为顶点的三角形与△ABC相似？

查看试题解析
22. 商城某种商品平均每天可销售20件，每件盈利30元，为庆十一，决定进行促销活动，经调查发现，每件商品每降价1元，商场平均每天可多售出2件．设该商品每件降价x元，请解答下列问题：

(1)、用含x的代数式表示：①降价后每售一件盈利元；②降价后平均每天售出件；

(2)、若商城在促销活动中，计划每天盈利750元，并且使消费者得到更多实惠，每件商品应降价多少元？（列方程解答）

(3)、在此次促销活动中，商城若要获得最大盈利，每件商品应降价多少元？获得最大盈利多少元？

查看试题解析
23. 如图，抛物线 $y = - \frac{1}{2} x^{2} + \frac{5}{2} x - 2$ 与 $x$ 轴相交于 $A ， B$ ，与 $y$ 轴相交于点 $C$ ，过点C作 $C D / / x$ 轴，交抛物线于点 $D$ .

(1)、求梯形ACDB的面积；

(2)、若梯形ACDB的对角线 $A D ， B C$ 交于点 $E$ ，求点 $E$ 的坐标，并求经过 $A ， B ， E$ 三点的抛物线的解析式； .

(3)、点 $P$ 是射线 $C D$ 上一点，且 $△ P B C$ 与 $△ A B C$ 相似，求符合条件的 $P$ 点坐标.

查看试题解析