安徽省安庆市2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 将抛物线y=x2-2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是( )A、y=x2-2x-1 B、y=x2+2x-1 C、y=x2-2 D、y=x2+22. 若 = ,则下列各式不成立的是( )A、 = B、 = C、 = D、 =3. 如图,已知一次函数y=ax+b与反比例函数y= 图象交于M、N两点,则不等式ax+b> 解集为( )
 A、x>2或﹣1<x<0 B、﹣1<x<0 C、﹣1<x<0或0<x<2 D、x>24. 如图,已知 、 分别是 的 、 边上的点, ,且 四边形 =1:8,那么 等于( )
A、x>2或﹣1<x<0 B、﹣1<x<0 C、﹣1<x<0或0<x<2 D、x>24. 如图,已知 、 分别是 的 、 边上的点, ,且 四边形 =1:8,那么 等于( ) A、 B、 C、 D、5. 如图, 为反比例函数 图象上一点, 垂直于 轴于点 ,若 ,则 的值为( )
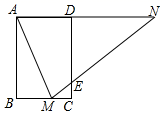
A、 B、 C、 D、5. 如图, 为反比例函数 图象上一点, 垂直于 轴于点 ,若 ,则 的值为( ) A、-6 B、-3 C、 D、不能确定6. 已知 , , 在函数 的图象上,则 , , 的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y1>y2 D、y2>y1>y37. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、
A、-6 B、-3 C、 D、不能确定6. 已知 , , 在函数 的图象上,则 , , 的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y1>y2 D、y2>y1>y37. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、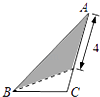 B、
B、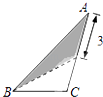 C、
C、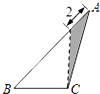 D、
D、 8. 已知二次函数 的 与 的部分对应值如下表:
8. 已知二次函数 的 与 的部分对应值如下表:-1
0
1
3
-3
1
3
1
下列结论:①抛物线的开口向下;②其图象的对称轴为 ;③当 时,函数值 随 的增大而增大;④方程 有一个根大于4;⑤若 ,且 ,则 .其中正确的结论有( )
A、①②③ B、①②③④⑤ C、①③⑤ D、①③④⑤9. 如图,在矩形ABCD中, , ,当直角三角板MPN的直角顶点P在BC边上移动时,直角边MP始终经过点A,设直角三角板的另一直角边PN与CD相交于点 , ,那么y与x之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
10. 已知函数 ,当 时,它是二次函数.11. 如图,小明在A时测得某树的影长为3米,B时又测得该树的影长为12米,若两次日照的光线互相垂直,则树的高度为米.
 12. 如图,一名男生推铅球,铅球行进高度 (单位: )与水平距离 (单位: )之间的关系是 ,则他将铅球推出的距离是 .
12. 如图,一名男生推铅球,铅球行进高度 (单位: )与水平距离 (单位: )之间的关系是 ,则他将铅球推出的距离是 .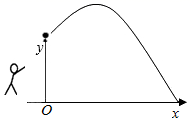 13. 如图,在 中, , , , , 分别为 、 上的点,沿直线 将 折叠,使点B恰好落在 上的 处,当 恰好为直角三角形时,BE的长为 .
13. 如图,在 中, , , , , 分别为 、 上的点,沿直线 将 折叠,使点B恰好落在 上的 处,当 恰好为直角三角形时,BE的长为 .
三、解答题
-
14. 已知二次函数y=﹣2x2﹣4x+6.(1)、用配方法求出函数的顶点坐标;(2)、将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.15. “今有井径五尺,不知其深,立五尺于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,求井深BD.
 16. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中.
16. 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中. (1)、求这条抛物线所对应的函数关系式;(2)、一辆宽为2米,高为3米的货船能否从桥下通过?17. 如图,一次函数y1=﹣x+5与反比例函数y2= 的图象交于A(1,m)、B(4,n)两点.
(1)、求这条抛物线所对应的函数关系式;(2)、一辆宽为2米,高为3米的货船能否从桥下通过?17. 如图,一次函数y1=﹣x+5与反比例函数y2= 的图象交于A(1,m)、B(4,n)两点. (1)、求A、B两点的坐标和反比例函数的解析式;(2)、求△AOB的面积.18. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、求A、B两点的坐标和反比例函数的解析式;(2)、求△AOB的面积.18. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.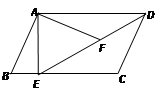 (1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.19. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.(1)、求抛物线y=x2﹣2x+2与x轴的“和谐值”;(2)、求抛物线y=x2﹣2x+2与直线y=x﹣1的“和谐值”.20. 如图在锐角 中, ,高 ,两动点 、 分别在 、 上滑动(不包含端点),且 ,以 为边长向下作正方形 ,设 ,正方形 与 公共部分的面积为 .
(1)、求证:△ADF∽△DEC(2)、若AB=4,AD=3 ,AE=3,求AF的长.19. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”.(1)、求抛物线y=x2﹣2x+2与x轴的“和谐值”;(2)、求抛物线y=x2﹣2x+2与直线y=x﹣1的“和谐值”.20. 如图在锐角 中, ,高 ,两动点 、 分别在 、 上滑动(不包含端点),且 ,以 为边长向下作正方形 ,设 ,正方形 与 公共部分的面积为 .
 (1)、如图(1),当正方形 的边 恰好落在 边上时,求 的值.(2)、如图(2),当 落 外部时,求出 与 的函数关系式(写出 的取值范围)并求出 为何值时 最大,最大是多少?
(1)、如图(1),当正方形 的边 恰好落在 边上时,求 的值.(2)、如图(2),当 落 外部时,求出 与 的函数关系式(写出 的取值范围)并求出 为何值时 最大,最大是多少?