黑龙江省哈尔滨市2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 下列方程中,是一元一次方程的是( )A、 B、 C、 D、2. 下列方程中的解是 的是( )A、 B、 C、 D、3. 下列各图中,∠1与∠2是对顶角的是( )A、
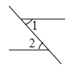 B、
B、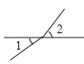 C、
C、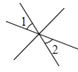 D、
D、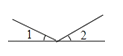 4. 在下列图形中,由∠1=∠2 能得到 AB∥CD 的是( )A、
4. 在下列图形中,由∠1=∠2 能得到 AB∥CD 的是( )A、 B、
B、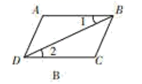 C、
C、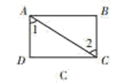 D、
D、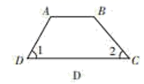 5. 在解方程 时,去括号正确的是( )A、 B、 C、 D、6. 如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
5. 在解方程 时,去括号正确的是( )A、 B、 C、 D、6. 如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( ) A、∠C=∠CDE B、∠ABD=∠CBD C、∠ABD=∠CDB D、∠C+∠ADC=180°7. 如图, ,则 , ,则 的大小是
A、∠C=∠CDE B、∠ABD=∠CBD C、∠ABD=∠CDB D、∠C+∠ADC=180°7. 如图, ,则 , ,则 的大小是 A、30° B、40° C、50° D、60°8. 已知x=2是关于x的方程 的一个解,则2a-1的值是( )A、1 B、2 C、3 D、49. 某种商品的标价为120元,若以九折降价出售,相对于进价仍获利20%,则该商品的进价是( ).A、95元 B、90元 C、85元 D、80元10. 下列四个命题:①如果∠A=∠B,那么∠A与∠B是对顶角;②过一点有且只有一条直线与已知直线平行;③同位角相等,两直线平行;④互相垂直的两条线段一定相交,其中正确的个数是( )A、1 B、2 C、3 D、4
A、30° B、40° C、50° D、60°8. 已知x=2是关于x的方程 的一个解,则2a-1的值是( )A、1 B、2 C、3 D、49. 某种商品的标价为120元,若以九折降价出售,相对于进价仍获利20%,则该商品的进价是( ).A、95元 B、90元 C、85元 D、80元10. 下列四个命题:①如果∠A=∠B,那么∠A与∠B是对顶角;②过一点有且只有一条直线与已知直线平行;③同位角相等,两直线平行;④互相垂直的两条线段一定相交,其中正确的个数是( )A、1 B、2 C、3 D、4二、填空题
-
11. 列等式表示:比b的一半小7的数等于a与b的和 .12. 把命题“两直线平行,内错角相等”改成“如果……那么……”的形式:13. 当x=时, 的值是2.14. 如图,要把池中的水引到D处,可过D点作CD⊥AB于C,然后沿CD开渠,可使所开渠道最短,试说明设计的依据:。
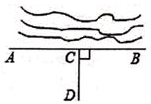 15. 如图,长8米宽6米的草坪上有一条弯折的小路(小路进出口的宽度相等,且每段小路均为平行四边形),小路进出口的宽度均为1米,则小路的面积为平方米.
15. 如图,长8米宽6米的草坪上有一条弯折的小路(小路进出口的宽度相等,且每段小路均为平行四边形),小路进出口的宽度均为1米,则小路的面积为平方米. 16. 如图,已知AB、CD相交于点O,OE⊥AB于O,∠EOC=28°,则∠AOD=度;
16. 如图,已知AB、CD相交于点O,OE⊥AB于O,∠EOC=28°,则∠AOD=度;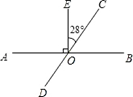 17. 如图,AB∥CD,∠B=34°,∠D=41°,则∠BED的度数为.
17. 如图,AB∥CD,∠B=34°,∠D=41°,则∠BED的度数为. 18. 甲、乙两人练习赛跑,甲每秒跑7米乙每秒跑6米,甲让乙先跑6米,问秒后甲可追上乙.19. 在平面内,已知∠AOB=50°,OC⊥OA,OD平分∠BOC,则∠AOD的度数为.20. 如图BE∥CF,BC⊥CD,A为CB延长线上一点,若∠ABE -∠DCF=20°,则∠CBE=.
18. 甲、乙两人练习赛跑,甲每秒跑7米乙每秒跑6米,甲让乙先跑6米,问秒后甲可追上乙.19. 在平面内,已知∠AOB=50°,OC⊥OA,OD平分∠BOC,则∠AOD的度数为.20. 如图BE∥CF,BC⊥CD,A为CB延长线上一点,若∠ABE -∠DCF=20°,则∠CBE=.
三、解答题
-
21. 计算:(1)、(2)、22. 如图,网格中每个小正方形的边长均为1,点A、B、C均在小正方形的顶点上.
 (1)、过点C作CM⊥AB,垂足为M;(2)、平移△ABC,使点C平移到点M,点A的对应点为点E,点B的对应点为点F,画出平移后的△MEF;(3)、连接CF,直接写出△CBF的面积为.23. 完成下面的推理过程.
(1)、过点C作CM⊥AB,垂足为M;(2)、平移△ABC,使点C平移到点M,点A的对应点为点E,点B的对应点为点F,画出平移后的△MEF;(3)、连接CF,直接写出△CBF的面积为.23. 完成下面的推理过程.如图,AB∥CD,BE、CF分别是∠ABC和∠BCD的平分线.求证:∠E=∠F
证明:∵AB∥CD(已知)
∴∠ABC=∠BCD( )
∵BE、CF分别是∠ABC和∠BCD的平分线(已知)
∴∠CBE= ∠ABC,∠BCF= ∠BCD( )
∴∠CBE=∠BCF( )
∴BE∥CF( )
∴∠E=∠F( )
 24. 如图所示,直线AB、CD相交于点O,
24. 如图所示,直线AB、CD相交于点O, (1)、若∠AOC+∠BOD=90°,求∠BOC的度数(2)、若∠BOC比∠AOC的2倍多33°,求∠AOC的度数.25. 哈尔滨实验学校为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买1副围棋和1副中国象棋需用26元;若购买8副围棋和3副中国象棋需用158元;(1)、求每副围棋和每副中国象棋各多少元;(2)、实验中学决定购买围棋和中国象棋共40副,总费用550元,那么实验中学可以购买多少副围棋.26. 如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.
(1)、若∠AOC+∠BOD=90°,求∠BOC的度数(2)、若∠BOC比∠AOC的2倍多33°,求∠AOC的度数.25. 哈尔滨实验学校为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买1副围棋和1副中国象棋需用26元;若购买8副围棋和3副中国象棋需用158元;(1)、求每副围棋和每副中国象棋各多少元;(2)、实验中学决定购买围棋和中国象棋共40副,总费用550元,那么实验中学可以购买多少副围棋.26. 如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.

 (1)、求证:∠EHC+∠GFE=180°.(2)、如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.(3)、如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数.27. 2019年寒假即将到来,哈尔滨实验学校准备组织七年级学生参观冰雪大世界.参观门票学生票价为160元;冰雪大世界经营方为学校活动推出两种优惠方案,方案一:“所有学生门票一律九折”。方案二:“若学生人数超过100人,则超出的部分打八折”。(1)、设学校有学生x人,用x分别表示方案一和方案二的费用.(2)、学校为了能使学生安全快捷到达冰雪大世界,现准备集体租车去冰雪大世界,若单独租45座的客车若干辆,则有15人没有座位:若租同样数量60座的客车,则多出一辆,且其余客车恰好坐满,求七年级学生有多少人参观冰雪大世界;(3)、在(2)的条件下,学校采用哪种优惠方案购买门票省钱,门票费用最低是多少.
(1)、求证:∠EHC+∠GFE=180°.(2)、如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.(3)、如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数.27. 2019年寒假即将到来,哈尔滨实验学校准备组织七年级学生参观冰雪大世界.参观门票学生票价为160元;冰雪大世界经营方为学校活动推出两种优惠方案,方案一:“所有学生门票一律九折”。方案二:“若学生人数超过100人,则超出的部分打八折”。(1)、设学校有学生x人,用x分别表示方案一和方案二的费用.(2)、学校为了能使学生安全快捷到达冰雪大世界,现准备集体租车去冰雪大世界,若单独租45座的客车若干辆,则有15人没有座位:若租同样数量60座的客车,则多出一辆,且其余客车恰好坐满,求七年级学生有多少人参观冰雪大世界;(3)、在(2)的条件下,学校采用哪种优惠方案购买门票省钱,门票费用最低是多少.