吉林省长春市南关区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 下列式子为最简二次根式的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 用配方法解一元二次方程: ,下列变形正确的是( )A、 B、 C、 D、4. 一元二次方程 根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 已知关于x的方程x2+x﹣a=0的一个根为2,则另一个根是( )A、﹣3 B、﹣2 C、3 D、66. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论错误的是( )
 A、 B、 C、 D、7. 如图,直线 ,直线 与这三条平行线分别交于点 和点 .若 ,则 的值为( )
A、 B、 C、 D、7. 如图,直线 ,直线 与这三条平行线分别交于点 和点 .若 ,则 的值为( ) A、 B、4 C、 D、8. 如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A、 B、4 C、 D、8. 如图,在 中, ,将 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 使二次根式 有意义的x的取值范围是.10. 计算: .11. 若 ,则 .12. 某市养老机构的养老床位数从2016年底的2万个增长到2018年底的2.88万个,求该市这两年(从2016年底到2018年底)拥有的养老床位数的平均年增长率.若设养老床位数的平均年增长率x,则所列方程为 .13. 如图,有一斜坡 ,坡顶B离地面的高度 为 ,斜坡的倾斜角是 ,若 ,则此斜坡的 为m.
 14. 如图,P是 内一点,连结P于 各顶点, 各顶点分别在边 、 、 、 上,且 .若 的面积为27,则 与 的面积和为 .
14. 如图,P是 内一点,连结P于 各顶点, 各顶点分别在边 、 、 、 上,且 .若 的面积为27,则 与 的面积和为 .
三、解答题
-
15. 计算: .16. 解方程: (用公式法)17. 阅读下列解答过程,在横线上填上恰当的内容
⑴由上述过程可知a的取值范围是 .
⑵上述解答过程有错误的是第步,正确结果为 .
18. 在如图所示的中面直角坐标系 中,每个小正方形的边长为1,每个小正方形的顶点叫做格点, 的顶点在正方形网格的格点上.顶点 的坐标分别为 、 、 . (1)、以点O为位似中心,在点O的异侧将 缩小为原来的 ,得到 .请画出 .(2)、 .(3)、设点 为 内一点,则依上述变换后,点P在 内的对应点 的坐标是 .19. 如图,一幅长 、宽 的矩形图案,其中有两条互相垂直的彩条,竖直彩条的宽度是水平彩条宽度的2倍,若图案中两条彩条所占面积是整个矩形图案面积的 .求彩条的宽度.
(1)、以点O为位似中心,在点O的异侧将 缩小为原来的 ,得到 .请画出 .(2)、 .(3)、设点 为 内一点,则依上述变换后,点P在 内的对应点 的坐标是 .19. 如图,一幅长 、宽 的矩形图案,其中有两条互相垂直的彩条,竖直彩条的宽度是水平彩条宽度的2倍,若图案中两条彩条所占面积是整个矩形图案面积的 .求彩条的宽度.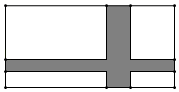 20. 如图,一台灯垂直于桌面的底座 的高为 ,台灯的支架 的长为 ,灯管 的长为 ,支架 与铅垂线 的夹角为 ,灯管 与水平线 的夹角为 ,求灯管顶端D到桌面的距离 .(结果精确到 )
20. 如图,一台灯垂直于桌面的底座 的高为 ,台灯的支架 的长为 ,灯管 的长为 ,支架 与铅垂线 的夹角为 ,灯管 与水平线 的夹角为 ,求灯管顶端D到桌面的距离 .(结果精确到 )(参考数据: , , , , , )
 21. 已知关于x的方程 .(1)、若此方程的一个根为 ,求k的值.(2)、求证:不论k取何实数,此方程都有两个不相等的实数根.22. 如图,在 中, 是 的延长线上点, 分别交 和 于点 .若 .
21. 已知关于x的方程 .(1)、若此方程的一个根为 ,求k的值.(2)、求证:不论k取何实数,此方程都有两个不相等的实数根.22. 如图,在 中, 是 的延长线上点, 分别交 和 于点 .若 . (1)、求证: ;(2)、求 的长.23. 如图①,平面内的两条直线 点 在直线 上,点 在直线 上,过 两点分别作 的垂线,垂足分别为 ,我们把线段 叫做线段 在直线 上的正投影,其长度可记为 或 特别地,线段 在直线 上的正投影就是线段 .请依据上述定义解决如下问题:
(1)、求证: ;(2)、求 的长.23. 如图①,平面内的两条直线 点 在直线 上,点 在直线 上,过 两点分别作 的垂线,垂足分别为 ,我们把线段 叫做线段 在直线 上的正投影,其长度可记为 或 特别地,线段 在直线 上的正投影就是线段 .请依据上述定义解决如下问题: (1)、如图①,若 ,则 .(2)、如图②,在矩形 中, , ,则 .(3)、如图③,在矩形 中,点E在 边上( ),连接 、 ,
(1)、如图①,若 ,则 .(2)、如图②,在矩形 中, , ,则 .(3)、如图③,在矩形 中,点E在 边上( ),连接 、 ,①若 ,求矩形 的面积.
②如图④,点F在 延长线上,连按 ,若 , , ,求 .
24. 如图,在 中, ,动点P从点A出发沿线段 以每秒3个单位长的速度运动至点B,过点P作 射线 于点Q.设点P的运动时间为t秒( ). (1)、线段 的长为(用含t的代数式表示)(2)、当 与 的周长的比为 时,求t的值.(3)、设 与 重叠部分图形的面积为S,求S与t之间的函数关系式.(4)、当直线 把 分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
(1)、线段 的长为(用含t的代数式表示)(2)、当 与 的周长的比为 时,求t的值.(3)、设 与 重叠部分图形的面积为S,求S与t之间的函数关系式.(4)、当直线 把 分成的两部分图形中有一个是轴对称图形时,直接写出t的值.