黑龙江省齐齐哈尔市龙沙区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 若1是关于x的一元二次方程 的一个根,则m值为( )A、-1 B、0 C、1 D、32. 下列图形中,是中心对称图形的是( )A、
 B、
B、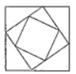 C、
C、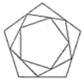 D、
D、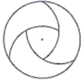 3. 关于x的一元二次方程 有两个不相等的实数根,则实数n的取值范围是( )A、 B、 C、 D、4. 用一个半径为6,圆心角为120°的扇形围成的圆锥的底面半径是( )A、1 B、2 C、3 D、45. 如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )
3. 关于x的一元二次方程 有两个不相等的实数根,则实数n的取值范围是( )A、 B、 C、 D、4. 用一个半径为6,圆心角为120°的扇形围成的圆锥的底面半径是( )A、1 B、2 C、3 D、45. 如图,在△ABC中,AB=8,AC=6,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1 , 连接BC1 , 则BC1的长为( )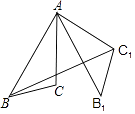 A、6 B、8 C、10 D、126. 已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )A、有最大值﹣1,有最小值﹣2 B、有最大值0,有最小值﹣1 C、有最大值7,有最小值﹣1 D、有最大值7,有最小值﹣27. 在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )A、
A、6 B、8 C、10 D、126. 已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )A、有最大值﹣1,有最小值﹣2 B、有最大值0,有最小值﹣1 C、有最大值7,有最小值﹣1 D、有最大值7,有最小值﹣27. 在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )A、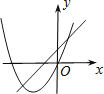 B、
B、 C、
C、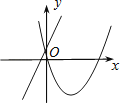 D、
D、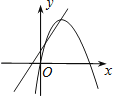 8. 某企业2018年初获利润300万元,到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是( )A、300(1+x)=507 B、300(1+x)2=507 C、300(1+x)+300(1+x)2=507 D、300+300(1+x)+300(1+x)2=5079. 如图,一条公路的转弯处是一段圆弧 ,点O是这段圆弧所在圆的圆心, ,点C是 的中点,点D是 的中点,且 ,则这段弯路所在圆的半径为( )
8. 某企业2018年初获利润300万元,到2020年初计划利润达到507万元.设这两年的年利润平均增长率为x.应列方程是( )A、300(1+x)=507 B、300(1+x)2=507 C、300(1+x)+300(1+x)2=507 D、300+300(1+x)+300(1+x)2=5079. 如图,一条公路的转弯处是一段圆弧 ,点O是这段圆弧所在圆的圆心, ,点C是 的中点,点D是 的中点,且 ,则这段弯路所在圆的半径为( )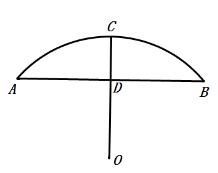 A、 B、 C、 D、10. 已知抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,有下列结论:① ;② ;③当 时,y随x增大而增大;④抛物线的顶点坐标为 ;⑤若方程 两根为 ( ),则 , .其中正确结论有( )
A、 B、 C、 D、10. 已知抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,有下列结论:① ;② ;③当 时,y随x增大而增大;④抛物线的顶点坐标为 ;⑤若方程 两根为 ( ),则 , .其中正确结论有( )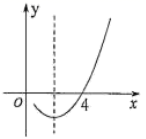 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
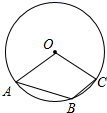
11. 写出一个图象开口向上,且经过点 的二次函数的解析式: .12. 同一个圆的内接正方形和正三角形的边心距的比为 .13. 如图,A、B、C是 上的三个点,若 ,则 .
 14. 将抛物线 向左平移2个单位得到的抛物线的顶点坐标为 .15. 如图,在 中, , , ,以 的中点O为圆心, 的长为半径作半圆交 于点D,则图中阴影部分的面积为 .
14. 将抛物线 向左平移2个单位得到的抛物线的顶点坐标为 .15. 如图,在 中, , , ,以 的中点O为圆心, 的长为半径作半圆交 于点D,则图中阴影部分的面积为 .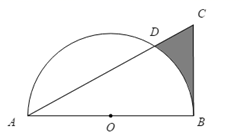 16. 一副三角板按如图所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当△ACD的一边与△AOB的某一边平行时,相应的旋转角α的值是.
16. 一副三角板按如图所示叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0°<α<180°),当△ACD的一边与△AOB的某一边平行时,相应的旋转角α的值是.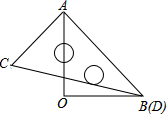 17. 如图放置的 都是边长为1的等边三角形,点 在 轴上,点 都在直线 上,则点 的坐标是.
17. 如图放置的 都是边长为1的等边三角形,点 在 轴上,点 都在直线 上,则点 的坐标是.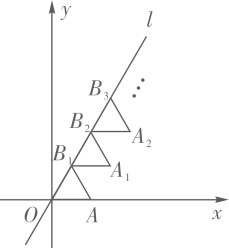
三、解答题
-
18. 解方程(1)、 .(2)、 .19. 已知关于x的一元二次方程 的两个实数根的平方和为12,求m的值.20. 如图,在 中, ,以 为直径的⊙O交 于点D,点E为 上一点,连接 、 , .
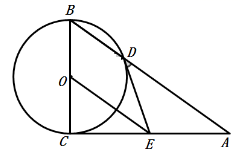 (1)、求证: 是⊙O的切线;(2)、若 ,⊙O半径为2,求 的长.21. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示支付方式有:A微信、B支付宝、C现金、D其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)、求证: 是⊙O的切线;(2)、若 ,⊙O半径为2,求 的长.21. 近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示支付方式有:A微信、B支付宝、C现金、D其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题: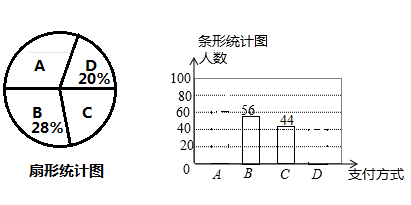 (1)、本次一共调查了名购买者?(2)、请补全条形统计图;在扇形统计图中,D种支付方式所对应的圆心角为度;(3)、若该超市这一周内有2000名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?22. 某商店销售一种商品,童威经市场调查发现:该商品的周销售量 (件)是售价 (元/件)的一次函数,其售价、周销售量、周销售利润 (元)的三组对应值如下表:
(1)、本次一共调查了名购买者?(2)、请补全条形统计图;在扇形统计图中,D种支付方式所对应的圆心角为度;(3)、若该超市这一周内有2000名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?22. 某商店销售一种商品,童威经市场调查发现:该商品的周销售量 (件)是售价 (元/件)的一次函数,其售价、周销售量、周销售利润 (元)的三组对应值如下表:售价 (元/件)
50
60
80
周销售量 (件)
100
80
40
周销售利润 (元)
1000
1600
1600
注:周销售利润=周销售量×(售价-进价)
(1)、①求 关于 的函数解析式(不要求写出自变量的取值范围)②该商品进价是元/件;当售价是元/件时,周销售利润最大,最大利润是元
(2)、由于某种原因,该商品进价提高了 元/件 ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求 的值23. 综合与实践如图,点E是正方形 的边 上一点,点P在线段 上,将线段 绕点E顺时针旋转90°得到线段 ,连接 ,过点E作 的垂线 ,垂足为点H,交射线 于点Q.
探究发现
 (1)、如图1,若点E是线段 的中点,直接写出线段 的数量关系为;(2)、如图2,若点E不是线段 的中点,线段 的数量关系为 , 填写出证明过程;(3)、当 , 时,连接 ,则 .24. 综合与探究
(1)、如图1,若点E是线段 的中点,直接写出线段 的数量关系为;(2)、如图2,若点E不是线段 的中点,线段 的数量关系为 , 填写出证明过程;(3)、当 , 时,连接 ,则 .24. 综合与探究如图,已知抛物线 与x轴交于A、 两点,与y轴交于点C,顶点坐标为点 .
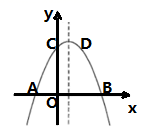 (1)、求此抛物线的解析式;(2)、点P为抛物线对称轴上一点,当 最小时,求点P坐标;(3)、在第一象限的抛物线上有一点M,当 面积最大时,求点M坐标;(4)、在x轴下方抛物线上有一点H, 面积为6,请直接写出点H的坐标.
(1)、求此抛物线的解析式;(2)、点P为抛物线对称轴上一点,当 最小时,求点P坐标;(3)、在第一象限的抛物线上有一点M,当 面积最大时,求点M坐标;(4)、在x轴下方抛物线上有一点H, 面积为6,请直接写出点H的坐标.