吉林省长春市榆树市2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 计算 的值是( )A、 B、 C、 D、2. 方程 的根是( )A、 , B、 , C、 D、3. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、4. 用配方法解方程 时,原方程应变形为( )A、 B、 C、 D、5. 做“抛掷一枚质地均匀的硬币试验”,在大量重复试验中,对于事件“正面朝上”的频率和概率,下列说法正确的是( )A、概率等于频率 B、频率等于 C、概率是随机的 D、频率会在某一个常数附近摆动6. 如图,要测量小河两岸相对的A,B两点之间的距离,可以在小河边取AB的垂线BC上的一点D,若测得BD=60米,∠ADB=40°,则AB等于( )
 A、60tan40°米 B、60tan50°米 C、60sin40°米 D、60sin50°米7. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )
A、60tan40°米 B、60tan50°米 C、60sin40°米 D、60sin50°米7. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )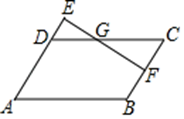 A、2:3 B、3:2 C、9:4 D、4:98. 据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺.人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山 位于树的西面.山高 为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一条直线上,人眼离地7尺.则山高 的长为(结果保留到整数,1丈=10尺)( )
A、2:3 B、3:2 C、9:4 D、4:98. 据《九章算术》记载:“今有山居木西,不知其高.山去五十三里,木高九丈五尺.人立木东三里,望木末适与山峰斜平.人目高七尺.问山高几何?”译文如下:如图,今有山 位于树的西面.山高 为未知数,山与树相距53里,树高9丈5尺.人站在离树3里的地方,观察到树梢C恰好与山峰A处在同一条直线上,人眼离地7尺.则山高 的长为(结果保留到整数,1丈=10尺)( )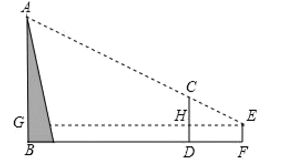 A、162丈 B、163丈 C、164丈 D、165丈
A、162丈 B、163丈 C、164丈 D、165丈二、填空题
-
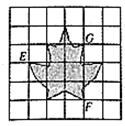
9. 计算: .10. 若式子 在实数范围内有意义,则 的取值范围是.11. 如图为正方形网格中的一片树叶,点 、 、 均在格点上,若点E的坐标为 ,点F的坐标为 ,则点G的坐标为.
 12. 如图,四边形 与四边形 关于点O成位似图形.若四边形 与四边形 的面积之比为 ,则它们的位似比为.
12. 如图,四边形 与四边形 关于点O成位似图形.若四边形 与四边形 的面积之比为 ,则它们的位似比为.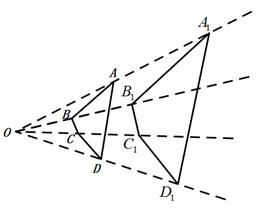 13. 如图,在平面直角坐标系中,O为坐标原点,点 在第一象限, 与x轴所夹的锐角为 ,且 ,则m的值是.
13. 如图,在平面直角坐标系中,O为坐标原点,点 在第一象限, 与x轴所夹的锐角为 ,且 ,则m的值是. 14. 如图, 是等腰直角三角形, , 为边 上一点,且 ,连结 ,过点C作 于点E,交 于点F.若 ,则 的长为.
14. 如图, 是等腰直角三角形, , 为边 上一点,且 ,连结 ,过点C作 于点E,交 于点F.若 ,则 的长为.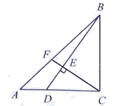
三、解答题
-
15. 计算: .16. 解方程: .17. 有三张正面分别标有数字-2,3,4的不透明卡片,它们除数字外都相同:现将它们背面朝上,洗匀后,从三张卡片中随机地抽出一张,记下数字后将卡片放回,洗匀后,再从这三张卡片中随机抽出一张,记下数字.用列表或画树状图的方法,求两次抽取的卡片上的数字符号不同的概率.18. 如图,在 的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,线段 的端点均在格点上,仅用无刻度的直尺,按下列要求完成画图,并保留作图痕迹.
 (1)、在图①中画一条射线 ,使 .(2)、在图②中画一条射线 ,使 .19. 如图,要设计一幅宽 ,长 的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为 ,如果要使所有彩条所占面积为原矩形图案面积的三分之一,求每个横彩条的宽度.
(1)、在图①中画一条射线 ,使 .(2)、在图②中画一条射线 ,使 .19. 如图,要设计一幅宽 ,长 的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为 ,如果要使所有彩条所占面积为原矩形图案面积的三分之一,求每个横彩条的宽度.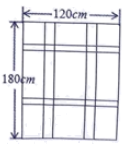 20. 如图,在 中, , , .D是边 中点,以点D为直角顶点向 上方作等腰直角三角形 ,边 经过点C, 与 交于点G.
20. 如图,在 中, , , .D是边 中点,以点D为直角顶点向 上方作等腰直角三角形 ,边 经过点C, 与 交于点G.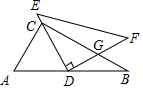 (1)、求 的长.(2)、若G为 的中点,求 的长.21. 如图, 和 是两个全等的等腰直角三角形, ,E为边 的中点,将 绕点E旋转,旋转过程中,边 与边 相交于点P,边 与边 延长线相交于点Q.
(1)、求 的长.(2)、若G为 的中点,求 的长.21. 如图, 和 是两个全等的等腰直角三角形, ,E为边 的中点,将 绕点E旋转,旋转过程中,边 与边 相交于点P,边 与边 延长线相交于点Q.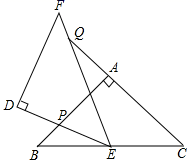 (1)、求证: .(2)、若 , ,求 的长.22. (教材呈现)下图是华师版九年级上册数学教材第78页的部分内容.
(1)、求证: .(2)、若 , ,求 的长.22. (教材呈现)下图是华师版九年级上册数学教材第78页的部分内容.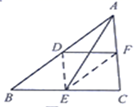
例1 求证:三角形的一条中位线与第三边上的中线互相平分.
已知:如图,在 中, , , .
求证: 、 互相平分.
证明:连结 、 .
(1)、请根据教材提示,结合图①,写出完整的解题过程.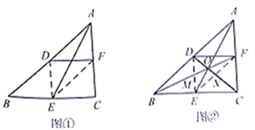 (2)、(结论应用)如图②,连结图①的 、 ,分别与 、 、 交于点M、N、O.
(2)、(结论应用)如图②,连结图①的 、 ,分别与 、 、 交于点M、N、O.若 ,求点M、N之间的距离.
(3)、若四边形 的面积为2,则 的面积为.23. 某数学兴趣小组为测量如图(①所示的一段古城墙的高度,设计用平面镜测量的示意图如图②所示,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处。 (1)、已知AB⊥BD、CD⊥BD,且测得AB=1.2m,BP=1.8m.PD=12m,求该城墙的高度(平面镜的原度忽略不计):(2)、请你设计一个测量这段古城墙高度的方案。
(1)、已知AB⊥BD、CD⊥BD,且测得AB=1.2m,BP=1.8m.PD=12m,求该城墙的高度(平面镜的原度忽略不计):(2)、请你设计一个测量这段古城墙高度的方案。要求:①面出示意图(不要求写画法);②写出方案,给出简要的计算过程:③给出的方案不能用到图②的方法。
24. 如图,在 中, , , .动点P以每秒5个单位长度的速度从点A出发,沿 的方向向终点C运动.点P关于点C的对称点为D,过点P作 于点Q,以 、 为边作 ,设点P的运动时间为 .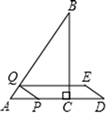 (1)、当点P在 上运动时,用含t的代数式表示 的长.(2)、当 为菱形时,求t的值.(3)、设 的面积为S,求S与t之间的函数关系式.(4)、作点E关于直线 的对称点 ,当点 落在 内部时,直接写出t的取值范围.
(1)、当点P在 上运动时,用含t的代数式表示 的长.(2)、当 为菱形时,求t的值.(3)、设 的面积为S,求S与t之间的函数关系式.(4)、作点E关于直线 的对称点 ,当点 落在 内部时,直接写出t的取值范围.