黑龙江省哈尔滨市呼兰区2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 等腰三角形的底角为 ,则它的顶角为( )A、 B、 C、 D、2. 如图,△ABC与△A'B'C'关于直线L对称,∠A=50°,∠C'=30°,则∠B的度数为( )
 A、30° B、50° C、90° D、100°3. 我们理应对我们所得的一切心怀感恩,这是我们强大的基础.少年强则国强,中国强则中国少年更强,中国强就是因为少年强.为了庆祝祖国生日小强做了以下几幅剪纸作品,其中是轴对称图形的是( )A、
A、30° B、50° C、90° D、100°3. 我们理应对我们所得的一切心怀感恩,这是我们强大的基础.少年强则国强,中国强则中国少年更强,中国强就是因为少年强.为了庆祝祖国生日小强做了以下几幅剪纸作品,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 点A(3,2)关于x轴对称的点的坐标为( )A、(3,-2 ) B、( -3,2) C、(-3,-2 ) D、( 3,2)5. 如图,AC=AD,BC=BD,则有( )
4. 点A(3,2)关于x轴对称的点的坐标为( )A、(3,-2 ) B、( -3,2) C、(-3,-2 ) D、( 3,2)5. 如图,AC=AD,BC=BD,则有( ) A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB6. 如图,在 中, 于点 , 垂直 交 于点 ,连接 ,若 , ,则 ( )
A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB6. 如图,在 中, 于点 , 垂直 交 于点 ,连接 ,若 , ,则 ( )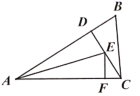 A、32° B、18° C、16°. D、29°7. 工人师傅常用角尺平分一个任意角,具体做法如下:如图,已知 是一个任意角,在边 , 上分别取 ,移动角尺两边相同的刻度分别与点 、 重合,则过角尺顶点 的射线 便是 角平分线.在证明 时运用的判定定理是( )
A、32° B、18° C、16°. D、29°7. 工人师傅常用角尺平分一个任意角,具体做法如下:如图,已知 是一个任意角,在边 , 上分别取 ,移动角尺两边相同的刻度分别与点 、 重合,则过角尺顶点 的射线 便是 角平分线.在证明 时运用的判定定理是( )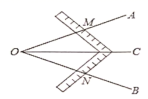 A、 B、 C、 D、8. 如图,等腰 的周长为17,底边 , 的垂直平分线 交 于点 ,交 于点 ,则 的周长为( )
A、 B、 C、 D、8. 如图,等腰 的周长为17,底边 , 的垂直平分线 交 于点 ,交 于点 ,则 的周长为( )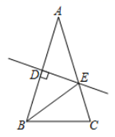 A、11 B、12 C、13 D、169. 如图,在等边 中,点 、 分别为 、 边上一点,连接 、 交于点 ,若 ,则 的度数是( )
A、11 B、12 C、13 D、169. 如图,在等边 中,点 、 分别为 、 边上一点,连接 、 交于点 ,若 ,则 的度数是( )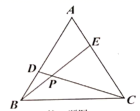 A、30° B、40° C、50° D、60°10. 如图,点 在 的内部,点 关于 、 的对称点分别为 、 ,连接 交 、 于点 、 ,若 ,则下列结论错误的是( )
A、30° B、40° C、50° D、60°10. 如图,点 在 的内部,点 关于 、 的对称点分别为 、 ,连接 交 、 于点 、 ,若 ,则下列结论错误的是( )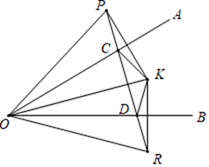 A、 B、 C、 D、 垂直平分
A、 B、 C、 D、 垂直平分二、填空题
-
11. 正方形有条对称轴.12. 如图, 是 的外角,则 .(填“>、<或=”)
 13. 如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则NP=海里.
13. 如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则NP=海里. 14. 如图,在 中, , 是 的角平分线,若 , ,则 的面积是 .
14. 如图,在 中, , 是 的角平分线,若 , ,则 的面积是 . 15. 如图,AB∥FC,E是DF的中点,若AB=20,CF=12,则BD=·
15. 如图,AB∥FC,E是DF的中点,若AB=20,CF=12,则BD=·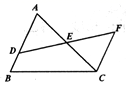 16. 如图,把一张长方形 的纸沿对角线 折叠,若 , ,则 的面积是 .
16. 如图,把一张长方形 的纸沿对角线 折叠,若 , ,则 的面积是 .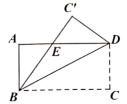 17. 如图,在 中, 、 分别平分 和 的外角, , ,则 .
17. 如图,在 中, 、 分别平分 和 的外角, , ,则 .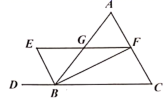 18. 如图,在△ABC中,BC=BA,∠ABC=120°,BD⊥BC交AC于点D,BD=1,则AC的长为.
18. 如图,在△ABC中,BC=BA,∠ABC=120°,BD⊥BC交AC于点D,BD=1,则AC的长为.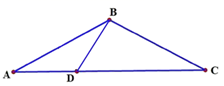 19. 在 中, , 点 在直线 上,若 ,则 的度数是 .20. 如图,在 中, ,点 在 上, ,连接 、 ,若 , ,则 .
19. 在 中, , 点 在直线 上,若 ,则 的度数是 .20. 如图,在 中, ,点 在 上, ,连接 、 ,若 , ,则 .
三、解答题
-
21. 如图,在 中, ,点 在边 上,且 ,连接 ,若 ,求 的度数.
 22. 如图, 的三个顶点坐标为 , , .
22. 如图, 的三个顶点坐标为 , , .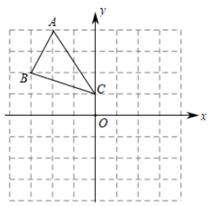 (1)、将 向右平移3个单位,得到 ,画出图形;(2)、作出 关于 轴对称的图形 ,并直接写出 点的坐标.23. 如图, , , ,连接 ,过点 作 于 ,过点 作 于 .
(1)、将 向右平移3个单位,得到 ,画出图形;(2)、作出 关于 轴对称的图形 ,并直接写出 点的坐标.23. 如图, , , ,连接 ,过点 作 于 ,过点 作 于 .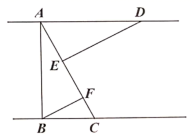 (1)、若 ,求 的度数.(2)、请直接写出线段 、 、 三者间的数量关系.24. 如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
(1)、若 ,求 的度数.(2)、请直接写出线段 、 、 三者间的数量关系.24. 如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.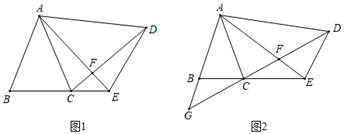 (1)、求证:BE=CD.(2)、当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.25. 如图,点 是 的平分线上一点, , , 、 是垂足,连接 交 于点 , .
(1)、求证:BE=CD.(2)、当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.25. 如图,点 是 的平分线上一点, , , 、 是垂足,连接 交 于点 , .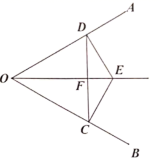 (1)、求证: 是等边三角形;(2)、若 , ,求 的长.26. 如图1,在 中, , 平分 ,连接 , , .
(1)、求证: 是等边三角形;(2)、若 , ,求 的长.26. 如图1,在 中, , 平分 ,连接 , , .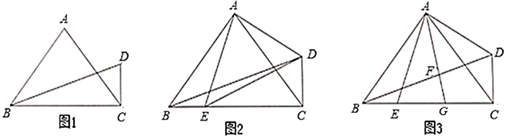 (1)、求 的度数:(2)、如图2,连接 , 交 于 ,连接 ,求证: ;(3)、如图3,在(2)的条件下,点 为 的中点,连接 交 于点 ,若 ,求线段 的长.27. 如图,在平面直角坐角系中,点 是原点,点 、 在坐标轴上,连接 , ,点 在 轴上,且点 是线段 的垂直平分线上一点.
(1)、求 的度数:(2)、如图2,连接 , 交 于 ,连接 ,求证: ;(3)、如图3,在(2)的条件下,点 为 的中点,连接 交 于点 ,若 ,求线段 的长.27. 如图,在平面直角坐角系中,点 是原点,点 、 在坐标轴上,连接 , ,点 在 轴上,且点 是线段 的垂直平分线上一点.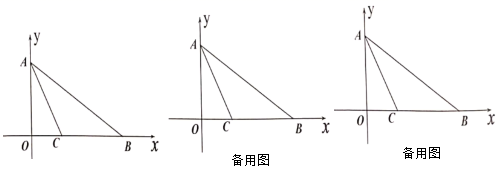 (1)、求点 的坐标;(2)、点 从点 出发以每秒2个单位长度的速度向终点 运动(点 不与点 重合),连接 、 ,若点 的运动时间为 秒, 的面积为 ,用含 的式子表示 ;(3)、在(2)的条件下,过点 作 垂直 轴,交 于 ,若 ,求点 的坐标.
(1)、求点 的坐标;(2)、点 从点 出发以每秒2个单位长度的速度向终点 运动(点 不与点 重合),连接 、 ,若点 的运动时间为 秒, 的面积为 ,用含 的式子表示 ;(3)、在(2)的条件下,过点 作 垂直 轴,交 于 ,若 ,求点 的坐标.