黑龙江省大庆市龙凤区2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
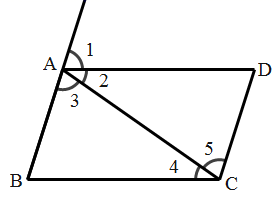
1. 下列计算正确的是( )A、 B、 C、 D、2. ( )A、 B、1 C、0 D、19973. 若 ,则 等于( )A、 B、 C、 D、4. 已知x+y=﹣5,xy=3,则x2+y2=( )A、25 B、﹣25 C、19 D、﹣195. 已知 ,则 ( )A、 B、 C、 D、526. 如图,在所标识的角中,同位角是( )
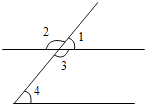 A、∠1和∠2 B、∠1和∠3 C、∠1和∠4 D、∠2和∠37. 下列说法错误的是( )A、过任意一点可作已知直线的一条平行线 B、同一平面内两条不相交的直线是平行线 C、在同一平面内,过直线外一点只能画一条直线与已知直线垂直 D、平行于同一直线的两直线平行8. 某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )A、第一次左拐30°,第二次右拐30° B、第一次右拐50°,第二次左拐130° C、第一次右拐50°,第二次右拐130° D、第一次向左拐50°,第二次向左拐120°9. 一杯开水凉了一段时间,那水温与时间的函数关系符合以下的图象中的( )A、
A、∠1和∠2 B、∠1和∠3 C、∠1和∠4 D、∠2和∠37. 下列说法错误的是( )A、过任意一点可作已知直线的一条平行线 B、同一平面内两条不相交的直线是平行线 C、在同一平面内,过直线外一点只能画一条直线与已知直线垂直 D、平行于同一直线的两直线平行8. 某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )A、第一次左拐30°,第二次右拐30° B、第一次右拐50°,第二次左拐130° C、第一次右拐50°,第二次右拐130° D、第一次向左拐50°,第二次向左拐120°9. 一杯开水凉了一段时间,那水温与时间的函数关系符合以下的图象中的( )A、 B、
B、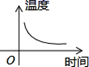 C、
C、 D、
D、 10. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
10. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )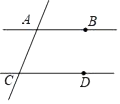 A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 计算: .12. 若 ,化简 .13. 已知等腰三角形的周长为60,底边长为x , 腰长为y , 则y与x之间的关系式 .14. 若 是一个完全平方式,则k=.15. 已知 ,则代数式 的值为 .16. 如图:若 , ,则 .
 17. 已知 与 ( , 都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且 ,则 的度数为 .18. 如图,在两个一大一小的正方形拼成的图形中,小正方形的面积是10平方厘米,阴影部分的面积为平方厘米.
17. 已知 与 ( , 都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且 ,则 的度数为 .18. 如图,在两个一大一小的正方形拼成的图形中,小正方形的面积是10平方厘米,阴影部分的面积为平方厘米.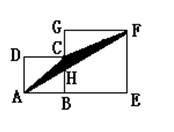
三、解答题
-
19. 计算:(1)、(2)、(3)、(4)、20. 先化简,再求值: ,其中 , .21. 化简求值: ,其中22. 已知如图, , , , .将下列推理过程补充完整:
⑴因为 (已知),所以 ()
⑵因为 (已知),所以 , ()
⑶因为 (已知),所以 , ()
 23. 甲、乙两山地自行车选手进行骑行训练.他们在同地出发,反向而行,分别前往A地和B地.甲先出发一分钟且先到达A地.两人到达目的地后均以原速按原路立即返回,直至两人相遇.下图是两人之间的距离y(千米)随乙出发时间x(分钟)之间的变化图象.请根据图象解决下列问题:
23. 甲、乙两山地自行车选手进行骑行训练.他们在同地出发,反向而行,分别前往A地和B地.甲先出发一分钟且先到达A地.两人到达目的地后均以原速按原路立即返回,直至两人相遇.下图是两人之间的距离y(千米)随乙出发时间x(分钟)之间的变化图象.请根据图象解决下列问题: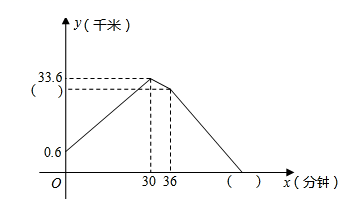 (1)、直接写出甲车和乙车的速度.(2)、在图中的两个括号内填上正确的数值.(3)、乙车出发多长时间两车首次相距22.6千米?
(1)、直接写出甲车和乙车的速度.(2)、在图中的两个括号内填上正确的数值.(3)、乙车出发多长时间两车首次相距22.6千米?

