吉林省长春市德惠市大学区2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、 -3 B、3 C、±3 D、81

查看试题解析
2. 如图，数轴上点N表示的数可能是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{7}$ D、 $\sqrt{10}$

查看试题解析
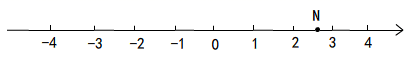3. 在实数0， $π$ ， $\frac{22}{7}$ ， $\sqrt{2}$ ，- $\sqrt{9}$ 中，无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 下列计算正确的是（）

A、 $a \cdot a = 2 a$ B、 ${(2 a)}^{2} = 2 a^{2}$ C、 ${(- a^{2})}^{3} = a^{6}$ D、 ${(- a^{3} b)}^{2} = a^{6} b^{2}$

查看试题解析
5. 下列命题中，是假命题的是（）

A、互补的两个角不能都是锐角 B、所有的直角都相等 C、乘积是1的两个数互为倒数 D、若a⊥b，a⊥c，则b⊥c

查看试题解析
6. 如图，一块三角形玻璃碎成了4块，现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃，那么最省事的办法是带哪块玻璃碎片去玻璃店？(　　)

A、① B、② C、③ D、④

查看试题解析
7. 工人师傅常用角尺平分一个任意角做法如下：如图所示，在∠AOB的两边OA ， OB上分别取OM＝ON ，移动角尺，使角尺两边相同的刻度分别与M ， N重合，过角尺顶点C的射线OC即是∠AOB的平分线画法中用到三角形全等的判定方法是（）

A、SSS B、SAS C、ASA D、HL

查看试题解析
8. 图（1）是一个长为2m，宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（）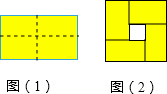

A、2mn B、（m+n）² C、（m-n）² D、m²-n²

查看试题解析

二、填空题

9. $- 3$ 的相反数是.

查看试题解析
10. 计算： ${(2 a^{3} b)}^{2} \div ab$ ＝.

查看试题解析
11. 因式分解： $2 a^{3} - 32 a =$ .

查看试题解析
12. 如图，将△ABC沿直线DE折叠后，使得点B与点A重合．已知AC＝5 cm，△ADC的周长为17 cm，则BC的长为．

查看试题解析
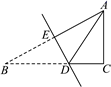13. 如图， $AB$ ＝ $AC$ ， $AD$ ＝ $AE$ ，∠ $BAC$ ＝∠ $DAE$ ，∠1＝35°，∠2＝30°，则∠3＝度.

查看试题解析
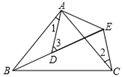14. 如图，在正方形网格中，每个小正方形的边长均为1，每个小正方形顶点叫做格点，△ABC的顶点都在格点上，以AB为一边作△ABP，使之与△ABC全等，从 $P_{1}$ 、 $P_{2}$ 、 $P_{3}$ 、 $P_{4}$ 四点中找出符合条件的点P，则点P有个

查看试题解析

三、解答题

15. 计算： $\sqrt{4} - \sqrt[3]{8} + \sqrt{1 \frac{7}{9}}$

查看试题解析
16. 因式分解： $4 a^{3} - 4 a^{2} b + {ab}^{2}$ .

查看试题解析
17. 先化简，再求值： ${(x + 1)}^{2} - (x + 2) (x - 2)$ ，其中 $x = - \frac{1}{2}$

查看试题解析
18. 如图，已知AB=AD，且AC平分∠BAD，求证：BC=DC

查看试题解析
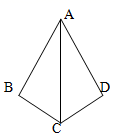19. 图①，图②均是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形顶点叫做格点，线段 $AB$ 、 $BC$ 的端点都在格点上.

(1)、在图①中找到一个格点，画出△ $ABD$ 和△ $BCD$ ，使△ $ABD$ 和△ $BCD$ 都是等腰三角形.
图①

(2)、在图②中找出一个格点E，画出△ $ABE$ 和△ $BCE$ ，使△ $ABE$ 和△ $BCE$ 全等.

图②

查看试题解析
20. 已知一个正数的平方根为2a﹣1和﹣a+2，求这个正数．

查看试题解析
21. 已 $x + y = 5, x y = 1$ ，求：

(1)、 $x^{2} + y^{2}$ ；

(2)、 ${(x - y)}^{2}$ .

查看试题解析
22. 如图，DE⊥AB于E ， DF⊥AC于F ，若BD＝CD ， BE＝CF ．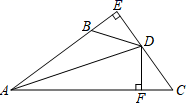

(1)、求证：AD平分∠BAC ．

(2)、写出AB+AC与AE之间的等量关系，并说明理由．

查看试题解析
23. 题目：如图①，在四边形ABCD中，AB＝AD，∠ABC＝∠ADC，那么BC＝CD吗？请说明理由.

小明的作法如下：

如图②，连结AC．

∵AB＝AD，∠ABC＝∠ADC，AC＝AC．

∴△ABC≌△ADC．

∴BC＝CD．

(1)、小明的作法错误的原因是.

(2)、请正确解答这道题目.

查看试题解析
24. 如图，△ABC是等边三角形，BC＝2 $c m$ .点P从点A出发沿沿射线AB以1 $c m / s$ 的速度运动，过点P作PE∥BC交射线AC于点E，同时点Q从点C出发沿BC的延长线以1 $c m / s$ 的速度运动，连结BE、EQ.设点P的运动时间为t（s）.

(1)、求证：△APE是等边三角形；

(2)、直接写出CE的长（用含t的代数式表示）；

(3)、当点P在边AB上，且不∵△ABC是等边三角形，

(4)、在不添加字母和连结其它线段的条件下，当图中等腰三角形的个数大于3时，直接写出t的值和对应的等腰三角形的个数.

查看试题解析