黑龙江省齐齐哈尔市铁锋区2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-07 类型:期中考试
一、单选题
-
1. 下列线段能组成三角形的是( )A、3、4、8 B、5、6、11 C、5、6、10 D、2、2、42. 下列大学的校徽图案是轴对称图形的是( )A、
 清华大学
B、
清华大学
B、 北京大学
C、
北京大学
C、 中国人民大学
D、
中国人民大学
D、 浙江大学
3. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( ).
浙江大学
3. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( ). A、SAS B、AAS C、ASA D、 SSS4. 若一个多边形的内角和为 ,则从此多边形的一个顶点出发可作的对角线共有( )A、5条 B、6条 C、7条 D、8条5. 等腰三角形的一个角是80°,则它的顶角的度数是( )A、80° B、80°或20° C、80°或50° D、20°6. 如图,在由等边三角形、正方形和正五边形组合而成的图形中,∠3=60°,则∠1+∠2的度数为( )
A、SAS B、AAS C、ASA D、 SSS4. 若一个多边形的内角和为 ,则从此多边形的一个顶点出发可作的对角线共有( )A、5条 B、6条 C、7条 D、8条5. 等腰三角形的一个角是80°,则它的顶角的度数是( )A、80° B、80°或20° C、80°或50° D、20°6. 如图,在由等边三角形、正方形和正五边形组合而成的图形中,∠3=60°,则∠1+∠2的度数为( ) A、39° B、40° C、41° D、42°7. 如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=5cm,BC=3cm,则△PBC的周长等于( )
A、39° B、40° C、41° D、42°7. 如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点,若AB=5cm,BC=3cm,则△PBC的周长等于( ) A、12cm B、11cm C、13cm D、8cm8. 用一批完全相同的多边形地砖铺地面,不能进行镶嵌的是( )A、正三角形 B、正方形 C、正八边形 D、正六边形9. 如图,是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选的位置有( )
A、12cm B、11cm C、13cm D、8cm8. 用一批完全相同的多边形地砖铺地面,不能进行镶嵌的是( )A、正三角形 B、正方形 C、正八边形 D、正六边形9. 如图,是三条两两相交的笔直公路,某物流公司现要修建一个货物中转站,使它到三条公路的距离相等,这个货物中转站可选的位置有( ) A、1个 B、3个 C、4个 D、5个10. 下列命题:①三角形三条高相交于一点;②斜边与一直角边分别相等的两个直角三角形全等;③两个锐角分别相等的两个直角三角形全等;④有两边及其中一边上的高分别相等的两个三角形全等;⑤三角形三边的垂直平分线相交于一点,且这点与三角形三个顶点的距离相等.其中真命题的个数有( )A、1个 B、2个 C、3个 D、4个
A、1个 B、3个 C、4个 D、5个10. 下列命题:①三角形三条高相交于一点;②斜边与一直角边分别相等的两个直角三角形全等;③两个锐角分别相等的两个直角三角形全等;④有两边及其中一边上的高分别相等的两个三角形全等;⑤三角形三边的垂直平分线相交于一点,且这点与三角形三个顶点的距离相等.其中真命题的个数有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 空调安装在墙上时,一般会用如图所示的三角形支架固定在墙上,这种方法应用的数学知识是.
 12. 如图,AC=BD,AC,BD交于点O,要使△ABC≌△DCB,只需添加一个条件,这个条件可以是 .
12. 如图,AC=BD,AC,BD交于点O,要使△ABC≌△DCB,只需添加一个条件,这个条件可以是 .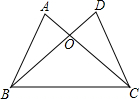 13. 如图,D、E、F分别为BC、AD、BE的中点,若△BFD的面积为6,则 △ABC的面积等于.
13. 如图,D、E、F分别为BC、AD、BE的中点,若△BFD的面积为6,则 △ABC的面积等于.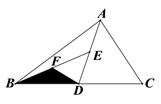 14. 如图,在 中, 与 的平分线交于点O,过点O作 ,分别交 、 于点M,N.若 , ,则 的周长为.
14. 如图,在 中, 与 的平分线交于点O,过点O作 ,分别交 、 于点M,N.若 , ,则 的周长为. 15. 已知在 中, ,高 、 所在直线相交于点P,则 度.16. 如图,在 中, , , ,点D是 边上一动点(不与点B、C重合),过点D作 交 边于点E,将 沿直线 翻折,点B落在射线 上的点F处,当 为直角三角形时, 的长为.
15. 已知在 中, ,高 、 所在直线相交于点P,则 度.16. 如图,在 中, , , ,点D是 边上一动点(不与点B、C重合),过点D作 交 边于点E,将 沿直线 翻折,点B落在射线 上的点F处,当 为直角三角形时, 的长为. 17. 在第1个 中, , ,在 上取一点 ,延长 到 ,使得 ;在 上取一点D,延长 到 ,使得 ;…,按此做法进行下去,第n个三角形的以 为顶点的内角的度数为.
17. 在第1个 中, , ,在 上取一点 ,延长 到 ,使得 ;在 上取一点D,延长 到 ,使得 ;…,按此做法进行下去,第n个三角形的以 为顶点的内角的度数为. 18. 已知:a,b,c为 的三边长.(1)、若a,b,c满足 ,试判断 的形状;(2)、化简: .19. 如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,AB=10cm,DC=3cm,试求△ABD的面积.
18. 已知:a,b,c为 的三边长.(1)、若a,b,c满足 ,试判断 的形状;(2)、化简: .19. 如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,AB=10cm,DC=3cm,试求△ABD的面积. 20. 已知:点O在 内部, , , .试用含 的式子表示 .
20. 已知:点O在 内部, , , .试用含 的式子表示 . 21. 如图所示,边长为1的正方形网格中, 的三个顶点A、B、C都在格点上.
21. 如图所示,边长为1的正方形网格中, 的三个顶点A、B、C都在格点上. (1)、作关于 关于x轴的对称图形 ,(其中A、B、C的对称点分别是D、E、F),并写出点D坐标;(2)、P为x轴上一点,请在图中画出使 的周长最小时的点P(不写画法,保留画图痕迹),并直接写出点P的坐标.22. 如图,在等边 中,AD是BC边上的中线,点E在线段AD上,连结BE,在BE的下方作等边 ,连结CF.
(1)、作关于 关于x轴的对称图形 ,(其中A、B、C的对称点分别是D、E、F),并写出点D坐标;(2)、P为x轴上一点,请在图中画出使 的周长最小时的点P(不写画法,保留画图痕迹),并直接写出点P的坐标.22. 如图,在等边 中,AD是BC边上的中线,点E在线段AD上,连结BE,在BE的下方作等边 ,连结CF. (1)、请写出AE与CF的数量关系,并证明你的结论;(2)、求 的度数.23. 综合与实践(1)、实践操作: 中, ,D为直线 上一点,过D点作 ,与直线 相交于点E,如图①,图②,图③所示,则 的形状为.
(1)、请写出AE与CF的数量关系,并证明你的结论;(2)、求 的度数.23. 综合与实践(1)、实践操作: 中, ,D为直线 上一点,过D点作 ,与直线 相交于点E,如图①,图②,图③所示,则 的形状为. (2)、问题解决:等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起解决问题.如图④, 中, ,E为 上一点,F为 延长线上一点,且 , 交 于D,求证: .
(2)、问题解决:等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起解决问题.如图④, 中, ,E为 上一点,F为 延长线上一点,且 , 交 于D,求证: . (3)、拓展与应用,在(2)的条件下,如图⑤,过点E作 的垂线,垂足为M,若 ,则 的长为.
(3)、拓展与应用,在(2)的条件下,如图⑤,过点E作 的垂线,垂足为M,若 ,则 的长为. 24. 综合与探究
24. 综合与探究如图,等腰直角 中, , ,现将该三角形放置在平面直角坐标系中,点B坐标为 ,点C坐标为 .
 (1)、过点A作 轴,求 的长及点A的坐标;(2)、连接 ,若P为坐标平面内异于点A的点,且以O、P、C为顶点的三角形与 全等,请直接写出满足条件的点P的坐标;(3)、已知 ,试探究在x轴上是否存在点Q,使 是以 为腰的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)、过点A作 轴,求 的长及点A的坐标;(2)、连接 ,若P为坐标平面内异于点A的点,且以O、P、C为顶点的三角形与 全等,请直接写出满足条件的点P的坐标;(3)、已知 ,试探究在x轴上是否存在点Q,使 是以 为腰的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.