初中数学人教版九年级上学期 第二十三章 23.2 中心对称
试卷更新日期:2020-09-07 类型:同步测试
一、单选题
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下图是用来证明勾股定理的图案被称为“赵爽弦图”,由四个全等的直角三角形和一个小正方形拼成的大正方形,对其对称性表述,正确的是( )
2. 下图是用来证明勾股定理的图案被称为“赵爽弦图”,由四个全等的直角三角形和一个小正方形拼成的大正方形,对其对称性表述,正确的是( ) A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形3. 如图,在4× 4的网格纸中,△ABC的三个顶点都在格点上.现要在这张网格纸中找出一格点作为旋转中心,绕着这个中心旋转后的三角形的顶点也在格点上,若旋转前后的两个三角形构成中心对称图形,那么满足条件的旋转中心有( )
A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形3. 如图,在4× 4的网格纸中,△ABC的三个顶点都在格点上.现要在这张网格纸中找出一格点作为旋转中心,绕着这个中心旋转后的三角形的顶点也在格点上,若旋转前后的两个三角形构成中心对称图形,那么满足条件的旋转中心有( )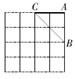 A、2个 B、3个 C、4个 D、20个4. 如图,△ABC与△ 关于点O成中心对称,则下列结论不成立的是( )
A、2个 B、3个 C、4个 D、20个4. 如图,△ABC与△ 关于点O成中心对称,则下列结论不成立的是( )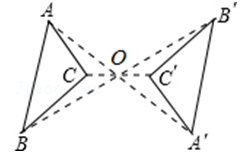 A、点A与点 是对称点 B、 C、AB∥ D、∠ACB=∠5. 在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,正六边形 ABCDEF的半径OA=OD=2,则点B关于原点O的对称点坐标为( )
A、点A与点 是对称点 B、 C、AB∥ D、∠ACB=∠5. 在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,正六边形 ABCDEF的半径OA=OD=2,则点B关于原点O的对称点坐标为( )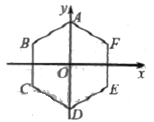 A、(1,- ) B、(-1, ) C、(- ,1) D、( ,-1)7. 如图,在正方形 中,顶点 在坐标轴上,且 ,以 为边构造菱形 .将菱形 与正方形 组成的图形绕点 逆时针旋转,每次旋转 ,则第2020次旋转结束时,点 的坐标为( )
A、(1,- ) B、(-1, ) C、(- ,1) D、( ,-1)7. 如图,在正方形 中,顶点 在坐标轴上,且 ,以 为边构造菱形 .将菱形 与正方形 组成的图形绕点 逆时针旋转,每次旋转 ,则第2020次旋转结束时,点 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
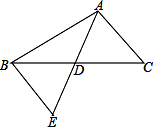
8. 如图, 和 关于点C成中心对称,若 , , ,则 的长是.
 9. 如图,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转°的角后,两张硬纸片所构成的图形是中心对称图形.
9. 如图,两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转°的角后,两张硬纸片所构成的图形是中心对称图形.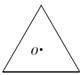 10. 给出如下5种图形:①矩形,②等边三角形,③正五边形,④圆,⑤线段.其中,是轴对称图形但不是中心对称图形的有.(请将所有符合题意的序号填在横线上)11. 已知点 与点 关于原点对称,则 .12. 若点A(2x﹣1,5)和点B(4,y+3)关于点(﹣3,2)对称,那么点A在第象限.13. 已知等边△ABC的重心为G , △DEF与△ABC关于点G成中心对称,将它们重叠部分的面积记作S1 , △ABC的面积记作S2 , 那么 的值是14. 如图,已知 与 成中心对称, 的面积是32,AB=16,则 中,CD边上的高为.
10. 给出如下5种图形:①矩形,②等边三角形,③正五边形,④圆,⑤线段.其中,是轴对称图形但不是中心对称图形的有.(请将所有符合题意的序号填在横线上)11. 已知点 与点 关于原点对称,则 .12. 若点A(2x﹣1,5)和点B(4,y+3)关于点(﹣3,2)对称,那么点A在第象限.13. 已知等边△ABC的重心为G , △DEF与△ABC关于点G成中心对称,将它们重叠部分的面积记作S1 , △ABC的面积记作S2 , 那么 的值是14. 如图,已知 与 成中心对称, 的面积是32,AB=16,则 中,CD边上的高为.
三、解答题
-
15. 如图,线段AC,BD相交于点O,AB //CD, :A B=CD.线段AC上的两点E,F关于点O中心对称.
求证:BF=DE.
 16. 如果B(m+1,3m﹣5)到x轴的距离与它到y轴的距离相等,求:(1)、m的值;(2)、求它关于原点的对称点坐标.17. 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
16. 如果B(m+1,3m﹣5)到x轴的距离与它到y轴的距离相等,求:(1)、m的值;(2)、求它关于原点的对称点坐标.17. 每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点0为对称中心,画出△ABC关于原点O对称的△A1B1C1 , 并写出A1、B1、C1的坐标.