四川省甘孜藏族自治州甘孜县2019-2020学年七年级上学期数学12月月考试卷

试卷更新日期：2020-09-04 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式中结果为负数的是（）．

A、 ${(- 3)}^{2}$ B、 $- 3^{2}$ C、 $- (- 3)$ D、| $- 3$ |

查看试题解析
2. 某商店举行促销活动，其促销的方式是“消费超过100元时，所购买的商品按原价打8折后，再减少20元”．若某商品的原价为x元（x＞100），则购买该商品实际付款的金额（单位：元）是（）

A、80%x﹣20 B、80%（x﹣20） C、20%x﹣20 D、20%（x﹣20）

查看试题解析
3. 在一些商场、饭店或写字楼中，常常能看到一种三翼式旋转门在圆柱体的空间內旋转．旋转门的三片旋转翼把空间等分成三个部分，如图是从上面俯视旋转门的平面图，两片旋转翼之间的角度是（）

A、100° B、120° C、135° D、150°

查看试题解析
4. 下列各式中是一元一次方程的是（）

A、 $\frac{1}{x}$ - 1 = 0 B、3 $y^{2}$ = 5 C、3x + y = 1 D、0.3 - 0.2 x = - x

查看试题解析
5. 如图，下列说法中错误的是（）

A、OA的方向是东北方向 B、OB的方向是北偏西60° C、OC的方向是南偏西60° D、OD的方向是南偏东60°

查看试题解析
6. 下列解方程步骤正确的是（）

A、由0.2x+4=0.3x+1，得0.2x-0.3x=1+4 B、由 $\frac{x}{4}$ +1= $\frac{0.3 x + 1}{0.1}$ +1.2，得 $\frac{x}{4}$ +1= $\frac{3 x + 10}{1}$ +12 C、由0.2x-0.3=2-1.3x ，得2x-3=2-13x D、由 $\frac{x - 1}{3}$ - $\frac{x + 2}{6}$ =2，得2x-2-x-2=12

查看试题解析
7. 若x=-3是方程 $2 (x - m) = 6$ 的解，则 $m$ 的值是（）

A、6 B、－6 C、12 D、－12

查看试题解析
8. 如图，是直角顶点重合的一副三角尺，若∠BCD=30°，下列结论错误的是（）

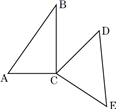A、∠ACD=120° B、∠ACD=∠BCE C、∠ACE=120° D、∠ACE-∠BCD=120°

查看试题解析
9. 时钟的时间是3点30分，时钟面上的时针与分针的夹角是（）

A、90° B、100° C、75° D、105°

查看试题解析
10. 如图，线段AB=BC=CD=DE=1cm，图中所有线段的长度之和为（）

A、25cm B、20cm C、15cm D、10cm

查看试题解析

二、填空题

11. 建筑工人在砌墙时，经常用细线绳在墙的两端之间拉一条参照线，使垒的每一层砖在一条直线上 $.$ 这样做的依据是：．

查看试题解析
12. 若4x﹣1与7﹣2x的值互为相反数，则x= ．

查看试题解析
13. 如果从一个多边形的一个顶点出发作它的对角线，最多能将多边形分成 2018 个三角形，那么这个多边形是边形.

查看试题解析
14. 如图，将一张纸张折叠，若∠1=65°，则∠2的度数为．

查看试题解析
15. 已知直线 l 上有三点 A ， B ， C ，线段 AB=10cm，BC=6cm，点 M 是线段 BC 的中点，则 AM=cm.

查看试题解析

三、解答题

16. 计算：

(1)、 $- 1^{2} - [2 - {(- 3)}^{2}] + {(- 1)}^{2}$

(2)、 $(1 \frac{3}{4} - 3 \frac{1}{2} - \frac{7}{12}) \times (- \frac{8}{7})$

查看试题解析
17. 先化简，再求值：

(1)、 $5 (3 a^{2} b - a b^{2}) - 4 (3 a^{2} b - a b^{2})$ ，其中 $a = 2$ ， $b = - 1$ ．

(2)、 $- 2 x^{2} + \frac{1}{2} [3 y^{2} - (2 x^{2} - y^{2}) + 12]$ ，其中 $x = - 1$ ， $y = - 2$

查看试题解析
18.

(1)、解方程： $4 x - 3 (20 - x) + 4 = 0$

(2)、解方程，并检验： $\frac{3 y - 1}{4} - 1 = \frac{5 y - 7}{6}$

查看试题解析
19. 画图题

(1)、如图，平面上有四个点 A、B、C、D，根据下列语句画图：
① 画直线 AB；

② 作射线 BC；

③ 画线段 CD；

④ 连接 DA 并延长，请使用直尺和圆规在线段 DA 的延长线上作线段 DE，使得 DE=2AD；

⑤ 数数看，此时图中共有（）条线段，以 A 为端点的射线共有（）条．

(2)、如图，有一只蚂蚁想从A点沿正方体的表面爬到G点，走哪一条路最近？请你利用部分平面展开图画出这条最短的路线，并说明理由．

查看试题解析
20. ① 如图（1），直线l上有2个点，则图中有2条可用图中字母表示的射线：A₁A₂、A₂A₁ ，有1条线段：A₁A₂；
② 如图（2），直线l上有3个点，则图中有几条可用图中字母表示的射线，有几条线段，并分别用图中字母表示出来；

③ 如图（3），直线l上有n个点，则图中有多少条可用图中字母表示的射线，有多少条线段，分别用含n的代数式表示出来；

④ 应用（3）中发现的规律解决问题：某校七年级共有8个班进行足球比赛，准备进行循环赛（即每两队之间赛一场），预计全部赛完共需多少场比赛？

查看试题解析
21. 观察下表：

我们把表格中字母的和所得的多项式称为"'特征多项式"，例如：第1格的“特征多项式”为 4x+y，第 2 格的“特征多项式”为 8x+4y，回答下列问题：

(1)、第 3 格的“特征多项式”为第 4 格的“待征多项式”为，第 n 格的“特征多项式”为.

(2)、若第 m 格的“特征多项式”与多项式-24x+2y-5 的和不含有 x 项，求此“特征多项式”.

查看试题解析
22. 已知点C是线段AB的中点

(1)、如图，若点D在线段CB上，且BD＝1.5厘米，AD＝6.5厘米，求线段CD的长度；

(2)、若将（1）中的“点D在线段CB上”改为“点D在线段CB的延长线上”，其他条件不变，请画出相应的示意图，并求出此时线段CD的长度．

查看试题解析
23. 已知点O在直线MN上，过点O作射线OP，使∠MOP=130°，将一块直角三角板的直角顶点始终放在点O处．

(1)、如图①，当三角板的一边OA在射线OM上，另一边OB在直线MN的上方时，求∠POB的度数；

(2)、若将三角板绕点O旋转至图②所示的位置，此时OB恰好平分∠PON，求∠BOP和∠AOM 的度数；

(3)、若将三角板绕点O旋转至图③所示位置，此时OA在∠PON 的内部，若OP所在的直线平分∠MOB，求∠POA 的度数；

查看试题解析