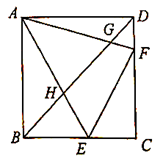
初中数学北师大版九年级上学期 第四章测试卷
试卷更新日期:2020-09-03 类型:单元试卷
一、单选题
-
1. 如图,AD∥BE∥CF,点B,E分别在AC,DF上,DE=2,EF=AB=3,则BC长为( )
 A、 B、2 C、 D、42. 如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A、 B、2 C、 D、42. 如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( ) A、28cm2 B、27cm2 C、21cm2 D、20cm23. 如图,在 中,D、E分别是AB和AC的中点, ,则 ( )
A、28cm2 B、27cm2 C、21cm2 D、20cm23. 如图,在 中,D、E分别是AB和AC的中点, ,则 ( )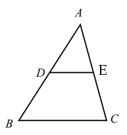 A、30 B、25 C、22.5 D、204. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )
A、30 B、25 C、22.5 D、204. 如图,在 中,点D在BC上,连接AD,点E在AC上,过点E作 ,交AD于点F,过点E作 ,交BC于点G,则下列式子一定正确的是( )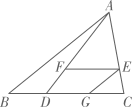 A、 B、 C、 D、5. 如图,在△ABC中,点E和点F分别在边AB,AC上,且EF∥BC,若AE=3,EB=6,BC=9,则EF的长为( )
A、 B、 C、 D、5. 如图,在△ABC中,点E和点F分别在边AB,AC上,且EF∥BC,若AE=3,EB=6,BC=9,则EF的长为( )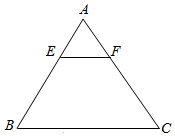 A、1 B、 C、 D、36. 如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
A、1 B、 C、 D、36. 如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )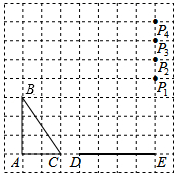 A、P1 B、P2 C、P3 D、P47. 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm , OA′=20cm , 则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )
A、P1 B、P2 C、P3 D、P47. 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm , OA′=20cm , 则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )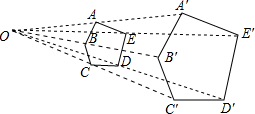 A、1:2 B、2:1 C、1:3 D、3:1
A、1:2 B、2:1 C、1:3 D、3:1二、填空题
-
8. 已知 ,则x:y:z= .9. 两个相似三角形的相似比为1:3,则它们周长的比为 .10. 如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E和点B,D,F,若AC=3,CE=6,BD=2,则DF的值是。
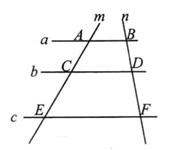 11. 如图, 且 ,则 的值为.
11. 如图, 且 ,则 的值为. 12. 我军侦察员在距敌方AN=120m的地方发现敌方的一座建筑物,但不知其高度,又不能靠近建筑物测量,机灵的侦察员将自己的食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住,如图所示.若此时眼睛到食指的距离AM约为40cm,食指BC的长约为8cm,则敌方建筑物DE的高度约是m。
12. 我军侦察员在距敌方AN=120m的地方发现敌方的一座建筑物,但不知其高度,又不能靠近建筑物测量,机灵的侦察员将自己的食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住,如图所示.若此时眼睛到食指的距离AM约为40cm,食指BC的长约为8cm,则敌方建筑物DE的高度约是m。
三、解答题
-
13. 小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
 14. 如图,已知 是坐标原点, 、 的坐标分别为 , .
14. 如图,已知 是坐标原点, 、 的坐标分别为 , . (1)、在 轴的左侧以 为位似中心作 的位似 ,使新图与原图的相似比为 ;(2)、分别写出 、 的对应点 、 的坐标.
(1)、在 轴的左侧以 为位似中心作 的位似 ,使新图与原图的相似比为 ;(2)、分别写出 、 的对应点 、 的坐标.四、综合题