初中数学北师大版九年级上学期 第四章 4.7 相似三角形的性质
试卷更新日期:2020-09-03 类型:同步测试
一、单选题
-
1. 已知 ,它们的周长分别为30和15,且 ,则 的长为A、3 B、2 C、4 D、52. 如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.
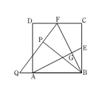
①AE⊥BF; ②QB=QF; ③ ; ④SECPG=3S△BGE
A、1 B、4 C、3 D、23. 若两个相似三角形的面积之比为1:4,则它们的周长之比为( )A、1:4 B、1:2 C、2:1 D、1:164. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为 ,则△ABC与△DEF对应中线的比为( )A、 B、 C、 D、5. 如图,平行四边形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是( )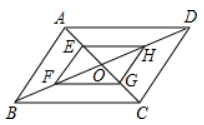 A、EH=HG B、四边形EFGH是平行四边形 C、AC⊥BD D、 的面积是 的面积的2倍6. 把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大 ;若边长扩大5倍,则面积扩大 。( )A、5倍,10倍 B、10倍,25倍 C、 倍,25倍 D、25倍,25倍
A、EH=HG B、四边形EFGH是平行四边形 C、AC⊥BD D、 的面积是 的面积的2倍6. 把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大 ;若边长扩大5倍,则面积扩大 。( )A、5倍,10倍 B、10倍,25倍 C、 倍,25倍 D、25倍,25倍二、填空题
-
7. △ABC与△DEF相似,其面积比为1:4,则它们的相似比为.8. ,其中点 分别与点 对应,如果 , ,那么 .9. 如图,已知△ABC∽△ADB,若AD=2,CD=2,则AB的长为.
 10. 如图,在阳光下,身高1.6m的小明站在旗杆AB影子的顶端C处,他立即沿CB的方向行走,走了5步,发现自己的影子顶端恰好也在C处,继续走了45步到达旗杆的底端B处,假设每步长度相等,则旗杆AB的高度为m.
10. 如图,在阳光下,身高1.6m的小明站在旗杆AB影子的顶端C处,他立即沿CB的方向行走,走了5步,发现自己的影子顶端恰好也在C处,继续走了45步到达旗杆的底端B处,假设每步长度相等,则旗杆AB的高度为m. 11. 如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为米.
11. 如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为米.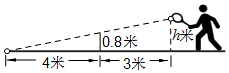
三、解答题
-
12. 如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在BC、CD上,若△ADE∽△CMN,求CM的长.
 13. 如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
13. 如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
四、作图题
-
14. 如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1.
 (1)、当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.(2)、如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)(3)、对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
(1)、当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.(2)、如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)(3)、对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?