初中数学北师大版九年级上学期 第四章 4.6 利用相似三角形测高
试卷更新日期：2020-09-03 类型：同步测试
一、单选题
-
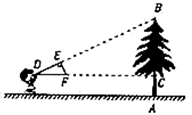
1. 如图，小明同学用自制的直角三角形纸板 测量树的高度 ，他调整自己的位置，设法使斜边 保持水平，并且边 与点 在同一直线上.已知纸板的两条直角边 ， ，测得边 离地面的高度 ， ，则树高 是（ ）
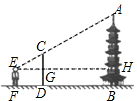
A、4米 B、4.5米 C、5米 D、5.5米2. 身高1.6米的小明同学利用相似三角形测量学校旗杆的高度，上午10点，小明在阳光下的影长为1米，此时测得旗杆的影长为9米，则学校旗杆的高度是（ ）A、 米 B、 米 C、 米 D、 米3. 路边有一根电线杆AB和一块长方形广告牌，有一天小明突然发现在太阳光照射下，电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处，而长方形广告牌的影子刚好落在地面上E点（如图），已知BC=5米，长方形广告牌的长HF=4米，高HC=3米，DE=4米，则电线杆AB的高度是（ ）
A、6.75米 B、7.75米 C、8.25米 D、10.75米4. AB和DE是直立在水平地面上的两根立柱，AB=7米，某一时刻测得在阳光下的投影 米，同时，测量出 在阳光下的投影长为6米，则DE的长为（ ）A、 米 B、 米 C、 米 D、 米5. 某数学活动小组在利用太阳光线测量某棵树 的高度时，发现树 的影子不全落在地面上，有一部分影子落在教学楼的墙壁上.经测量，落在墙壁上影高 为2米，落在地面上的影长 为5米，同一时间测得8米高的国旗杆影长是4米，则树高为（ ）
A、8米 B、10米 C、12米 D、14米6. 如图，小明为了测量高楼MN的高度，在离N点20米的A处放了一个平面镜，小明沿NA方向后退1.5米到C点，此时从镜子中恰好看到楼顶的M点，已知小明的眼睛（点B）到地面的高度BC是1.6米，则大楼MN的高度（精确到0.1米）约是（ ）
A、18.75米 B、18.8米 C、21.3米 D、19米7. 《孙子算经》是中国古代重要的数学著作，成书于约一千五百年前。其中有首歌谣：今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问竿长几何？意即：有一根竹竿不知道有多长，量出它在太阳下的影子长丈五尺．同时立一根一尺五寸的小标杆，它的影长五寸(提示：1丈=10尺，1尺=10寸)，则竹竿的长为（ ）
A、五丈 B、四丈五尺 C、一丈 D、五尺二、填空题
-
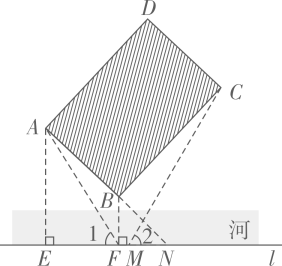
8. 如图，在河对岸有一矩形场地ABCD，为了估测场地大小，在笔直的河岸l上依次取点E，F，N，使AE⊥l，BF⊥l，点N，A，B在同一直线上。在F点观测A点后，沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米，FM=2米，MN=8米，∠ANE=45°，则场地的边AB为米，BC为米。
9. 小明在打网球时，为使球恰好能过网（网高0.8米），且落在对方区域离网5米的位置上，她的击球高度是2.4米，则她应站在离网的米处。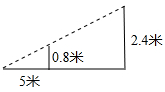
10. 如图是小玲用手电来测量城墙高度的示意图．在点P处水平放置平面镜，光线从点A出发经平面镜反射后，刚好射到城墙CD的顶端C处．已知AB⊥BD，CD⊥BD，且测得AB＝1.4米，BP＝2.1米，PD＝12米，则该城墙CD的高度米．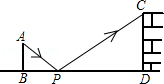
三、解答题
-
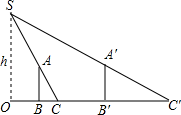
11. 为了测量路灯（OS）的高度，把一根长1.5米的竹竿（AB）竖直立在水平地面上，测得竹竿的影子（BC）长为1米，然后拿竹竿向远离路灯方向走了4米（BB′），再把竹竿竖立在地面上，测得竹竿的影长（B′C′）为1.8米，求路灯离地面的高度.
