初中数学北师大版九年级上学期 第四章 4.5 相似三角形判定定理的证明
试卷更新日期:2020-09-03 类型:同步测试
一、单选题
-
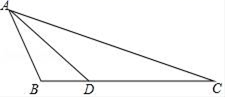
1. 如图,在 中, ,四边形 的面积为21,则 的面积是( )
 A、 B、25 C、35 D、632. 如图,正方形ABCD中,点E为BC右侧一点,∠AEC=90°,作DF⊥AE于点F,若CE=AF=2则正方形的面积为( )
A、 B、25 C、35 D、632. 如图,正方形ABCD中,点E为BC右侧一点,∠AEC=90°,作DF⊥AE于点F,若CE=AF=2则正方形的面积为( )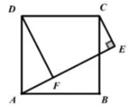 A、16 B、18 C、20 D、253. 如图,点D,E分别为△ABC边AB,AC上的一点,且DE∥BC,S△ADE=4,S四边形DBCE=5,则△ADE与△ABC相似比为( )
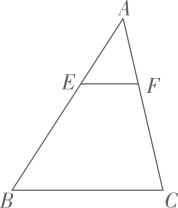
A、16 B、18 C、20 D、253. 如图,点D,E分别为△ABC边AB,AC上的一点,且DE∥BC,S△ADE=4,S四边形DBCE=5,则△ADE与△ABC相似比为( )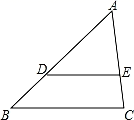 A、5:9 B、4:9 C、16:81 D、2:34. 如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比( )
A、5:9 B、4:9 C、16:81 D、2:34. 如图,在三角形ABC中,M,N分别是边AB,AC上的点,AM= AB,AN= AC,则三角形AMN的面积与四边形MBCN的面积比( )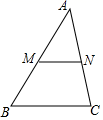 A、 B、 C、 D、5. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A、 B、 C、 D、5. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )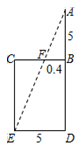 A、1.25尺 B、56.5尺 C、6.25尺 D、57.5尺6. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )
A、1.25尺 B、56.5尺 C、6.25尺 D、57.5尺6. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )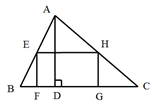 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
7. 如图,在 中,D是 中点, ,若 的周长为6,则 的周长为.
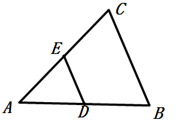 8. 如图,点C在 的内部,∠OCA=∠OCB , 与 互补,若 , ,则 .
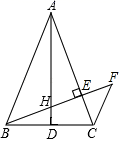
8. 如图,点C在 的内部,∠OCA=∠OCB , 与 互补,若 , ,则 . 9. 如图,在 中,已知 , ,垂足为D, .若 是 的中点,则 .
9. 如图,在 中,已知 , ,垂足为D, .若 是 的中点,则 .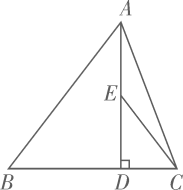 10. 如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=.
10. 如图,矩形ABCD中,AB=2,BC= ,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=.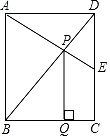 11. 如图所示,设G是△ABC的重心,过G的直线分别交AB,AC于点P,Q两点,则 =.
11. 如图所示,设G是△ABC的重心,过G的直线分别交AB,AC于点P,Q两点,则 =.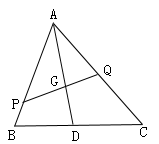 12. 如图,点D是△ABC的边AB上一点,如果∠ACD=∠B,并且 ,那么 .
12. 如图,点D是△ABC的边AB上一点,如果∠ACD=∠B,并且 ,那么 .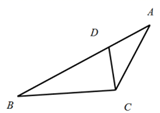
三、解答题
-
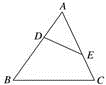
13. 已知如图,D,E分别是△ABC的边AB,AC上的点,AD=3,AB=8,AE=4,AC=6.求证:△ADE∽△ACB.
四、综合题