初中数学北师大版九年级上学期 第四章 4.4 探索三角形相似的条件
试卷更新日期:2020-09-03 类型:同步测试
一、单选题
-
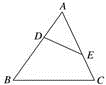
1. 如图,点 、 分别在 的边 、 上,且 与 不平行.下列条件中,能判定 与 相似的是( )
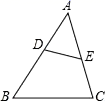 A、 B、 C、 D、2. 如图,点D、E分别在△ABC的AB、AC边上,下列条件中:①∠ADE=∠C;② ;③ .使△ADE与△ACB一定相似的是( )
A、 B、 C、 D、2. 如图,点D、E分别在△ABC的AB、AC边上,下列条件中:①∠ADE=∠C;② ;③ .使△ADE与△ACB一定相似的是( )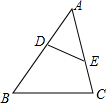 A、①② B、②③ C、①③ D、①②③3. 已知△ABC的三边长为8,12,18,又知△A1B1C1也有一边长为12,且与△ABC相似而不全等,则这样的△A1B1C1的个数为( )A、0 B、1 C、2 D、34. 如图,AB∥CD,AC,BD,EF相交于点O,则图中相似三角形共有( )
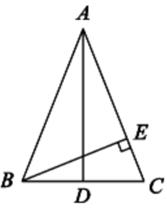
A、①② B、②③ C、①③ D、①②③3. 已知△ABC的三边长为8,12,18,又知△A1B1C1也有一边长为12,且与△ABC相似而不全等,则这样的△A1B1C1的个数为( )A、0 B、1 C、2 D、34. 如图,AB∥CD,AC,BD,EF相交于点O,则图中相似三角形共有( )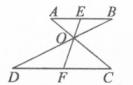 A、1对 B、2对 C、3对 D、4对5. 下列说法中正确的是( )A、两个等腰三角形相似 B、有一个内角是30°的两个直角三角形相似 C、有一个锐角是30°的两个等腰三角形相似 D、两个直角三角形相似6. 如图,在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
A、1对 B、2对 C、3对 D、4对5. 下列说法中正确的是( )A、两个等腰三角形相似 B、有一个内角是30°的两个直角三角形相似 C、有一个锐角是30°的两个等腰三角形相似 D、两个直角三角形相似6. 如图,在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )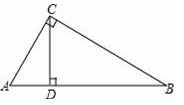 A、△ADC∽△ACB B、△BDC∽△BCA C、△ADC∽△CDB D、无法判断7. 如图,△ABC中,∠A=78°,AB=4,BC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A、△ADC∽△ACB B、△BDC∽△BCA C、△ADC∽△CDB D、无法判断7. 如图,△ABC中,∠A=78°,AB=4,BC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )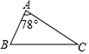 A、
A、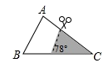 B、
B、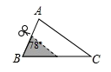 C、
C、 D、
D、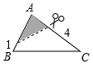 8. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
8. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、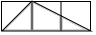 B、
B、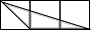 C、
C、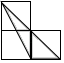 D、
D、 9. 下列两个三角形不一定相似的是( )A、两条直角边的比都是 的两个直角三角形 B、腰与底的比都是 的两个等腰三角形 C、有一个内角为 的两个直角三角形 D、有一个内角为 的两个等腰三角形
9. 下列两个三角形不一定相似的是( )A、两条直角边的比都是 的两个直角三角形 B、腰与底的比都是 的两个等腰三角形 C、有一个内角为 的两个直角三角形 D、有一个内角为 的两个等腰三角形二、填空题
-
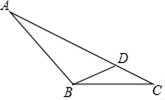
10. 如图,在△ABC与△AED中, ,添加一个条件,使△ABC与△AED相似,这个条件可以是。
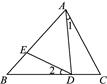
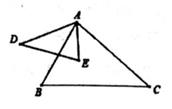 11. 如图,P为线段AB上一点,AD与BC交于E, ,BC交PD于F,AD交PC于G,则图中相似三角形有对.
11. 如图,P为线段AB上一点,AD与BC交于E, ,BC交PD于F,AD交PC于G,则图中相似三角形有对. 12. 如图,在正方形网格上有6个斜三角形:
12. 如图,在正方形网格上有6个斜三角形: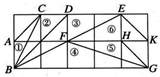
①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
在②~⑥中,与①相似的三角形的序号是.(把你认为正确的都填上)
三、解答题