山东省德州市宁津县2019-2020学年八年级上学期数学12月月考试卷

试卷更新日期：2020-09-03 类型：月考试卷

进入出卷网下载

一、单选题

1. 第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列线段，能组成三角形的是（）

A、2cm，3cm，5cm B、5cm，6cm，10cm C、1cm，1cm， 3cm D、3cm， 4cm， 8cm

查看试题解析
3. 在一个三角形中，一个外角是其相邻内角的3倍，那么这个外角是（）

A、150° B、135° C、120° D、100°

查看试题解析
4. 下列运算结果正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 $x^{3} \cdot x^{2} = x^{6}$ C、 $x^{5} \div x = x^{5}$ D、 $x^{3} \cdot {(3 x)}^{2} = 9 x^{5}$

查看试题解析
5. 下列运用平方差公式计算，错误的是（）

A、（a+b）（a﹣b）=a²﹣b² B、（2x+1）（2x﹣1）=2x²﹣1 C、（x+1）（x﹣1）=x²﹣1 D、（﹣3x+2）（﹣3x﹣2）=9x²﹣4

查看试题解析
6. 若 ${(a + b)}^{2} = {(a - b)}^{2} + A$ ，则A为（）

A、2ab B、-2ab C、4ab D、-4ab

查看试题解析
7. 下列各式能用平方差公式分解因式的有（）
①x²+y²；②x²﹣y²；③﹣x²﹣y²；④﹣x²+y²；⑤﹣x²+2xy﹣y² ．

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 到三角形三条边的距离相等的点是三角形（）的交点.

A、三条中线 B、三条角平分线 C、三条高 D、三条边的垂直平分线

查看试题解析
9. 下列关于两个三角形全等的说法：
①三个角对应相等的两个三角形全等②三条边对应相等的两个三角形全等③有两边和它们的夹角对应相等的两个三角形全等④有两边和其中一边上的高对应相等的两个三角形全等，正确的说法个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，直角坐标系中，点 A（ − 2，2）、B（0，1）点 P 在 x 轴上，且△PAB 的等腰三角形，则满足条件的点 P 共有（）个

A、1 B、2 C、3 D、4

查看试题解析
11. 若 $a^{2} - b^{2} = \frac{1}{6}$ ， $a - b = \frac{1}{2}$ ，则 $a + b$ 的值为（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、-3 D、3

查看试题解析
12. 如图，已知△ABE≌△ACD，下列选项中不能被证明的等式是（）

A、AD＝AE B、DB＝AE C、DF＝EF D、DB＝EC

查看试题解析

二、填空题

13. 一个凸多边形的内角和与外角和相等，它是边形．

查看试题解析
14. 分解因式：x²y﹣4xy+4y= ．

查看试题解析
15.
如图，△ABC≌△A′B′C′，其中∠A=36°，∠C′=24°，则∠B= ．

查看试题解析
16. 已知4y²+my+1是完全平方式，则常数m的值是．

查看试题解析
17. 如图，△ABC中，∠C=90°，BD平分∠ABC ，交AC于D ，若AB=10，CD=3，则△ABD的面积是．

查看试题解析
18. 已知 $2^{m} = a$ ， $32^{n} = b$ ， $m$ ， $n$ 为正整数，则 $2^{3 m + 10 n} =$ ．

查看试题解析

三、解答题

19. 分解因式：

(1)、 $6 x y^{2} - 9 x^{2} y - y^{3}$ ；

(2)、 $16 x^{4} - 1$

查看试题解析
20. 计算

(1)、 $(2 m + n) (2 m - n) - 2 {(m + n)}^{2}$

(2)、 ${(- 3 x^{2} y)}^{2} \cdot (6 x y^{3}) \div (9 x^{3} y^{4})$

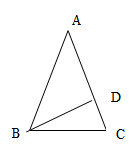
(3)、 ${(2 a^{2})}^{3} + {(- 3 a^{3})}^{2} + {(a^{2})}^{2} \cdot a^{2}$

查看试题解析
21. 如图，在ΔABC中，∠C=∠ABC=2∠A， BD是边AC上的高，求∠DBC的度数。

查看试题解析
22. 如图，点A、D、E在直线l上，∠BAC=90°，AB=AC，BD⊥l于D，CE⊥l于E，求证：DE=BD+CE.

查看试题解析
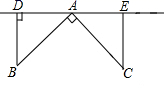23. 如图，已知Rt△ABC中，∠ACB=90°，CD⊥AB于D，∠BAC的平分线分别交BC、CD于E、F．

(1)、求证：∠ACD＝∠B

(2)、求证：△CEF是等腰三角形．

查看试题解析
24.

(1)、在图中作出△ABC关于y轴的对称图形△A₁B₁C₁；

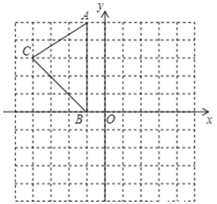(2)、写出点A₁、B₁、C₁的坐标；

(3)、在y轴上画出点P，使PA+PC最小．

查看试题解析
25. 已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．

(1)、（发现）
如图1，若∠ABC=∠ADC=90°，则∠BCD=°，△CBD是三角形；

(2)、（探索）
如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；

(3)、（应用）
如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有．（只填序号）

①2个②3个③4个④4个以上

查看试题解析