初中数学青岛版九年级上学期 第2章 2.5解直角三角形的应用
试卷更新日期:2020-09-02 类型:同步测试
一、单选题
-
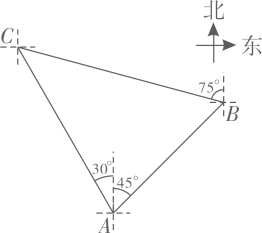
1. 如图所示,渔船在A处看到灯塔C在北偏东60º方向上,渔船向正东方向航行了12海里到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是( )
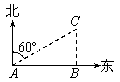 A、 海里 B、 海里 C、6海里 D、 海里2. 如图, 是河堤横断面的迎水坡,堤高 ,水平距离 ,则斜坡 的坡度为( )
A、 海里 B、 海里 C、6海里 D、 海里2. 如图, 是河堤横断面的迎水坡,堤高 ,水平距离 ,则斜坡 的坡度为( ) A、 B、 C、 D、3. 如图,要测量小河两岸相对的两点 之间的距离,可以在小河边 的垂线 上取一点C,测得 米, ,则 的长为( )
A、 B、 C、 D、3. 如图,要测量小河两岸相对的两点 之间的距离,可以在小河边 的垂线 上取一点C,测得 米, ,则 的长为( ) A、 米 B、 米 C、 米 D、 米4. 如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( )
A、 米 B、 米 C、 米 D、 米4. 如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1∶1.5,则坝底AD的长度为( )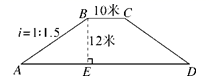 A、26米 B、28米 C、30米 D、46米5. 如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
A、26米 B、28米 C、30米 D、46米5. 如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( ) A、270cm B、210cm C、180cm D、96cm6. 如图,从A处观测铁塔顶部的仰角是30°,向前走30米到达B处,观测铁塔的顶部的仰角是45°,则铁塔高度是( )米
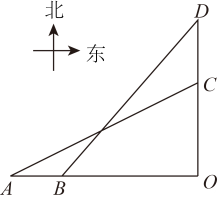
A、270cm B、210cm C、180cm D、96cm6. 如图,从A处观测铁塔顶部的仰角是30°,向前走30米到达B处,观测铁塔的顶部的仰角是45°,则铁塔高度是( )米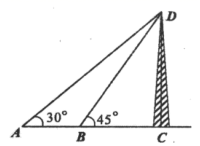 A、 B、 C、 D、7. 一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )
A、 B、 C、 D、7. 一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( ) A、(30 -50,30) B、(30,30 -50) C、(30 ,30) D、(30,30 )8. 如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18 m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )
A、(30 -50,30) B、(30,30 -50) C、(30 ,30) D、(30,30 )8. 如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18 m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是( )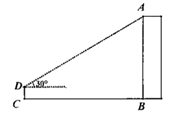 A、55.5m B、54m C、19.5m D、18m9. 如图为一节楼梯的示意图,BC⊥AC,∠BAC=α,AC=6米。现要在楼梯上铺一块地毯,楼梯宽度为1米,则地毯的面积至少需要( )平方米。
A、55.5m B、54m C、19.5m D、18m9. 如图为一节楼梯的示意图,BC⊥AC,∠BAC=α,AC=6米。现要在楼梯上铺一块地毯,楼梯宽度为1米,则地毯的面积至少需要( )平方米。 A、6tanα+6 B、 +6 C、 D、10. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角度数为α,看这栋楼底部C处的俯角度数为β,热气球A处与楼的水平距离为100m,则这栋楼的高度表示为( )
A、6tanα+6 B、 +6 C、 D、10. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角度数为α,看这栋楼底部C处的俯角度数为β,热气球A处与楼的水平距离为100m,则这栋楼的高度表示为( ) A、100(tanα+tanβ)m B、100(sinα+sinβ)m C、 D、11. 如图,在距离铁轨200米处的 处,观察由南宁开往百色的“和谐号”动车,当动车车头在 处时,恰好位于 处的北偏东 方向上,10秒钟后,动车车头到达 处,恰好位于 处西北方向上,则这时段动车的平均速度是( )米/秒.
A、100(tanα+tanβ)m B、100(sinα+sinβ)m C、 D、11. 如图,在距离铁轨200米处的 处,观察由南宁开往百色的“和谐号”动车,当动车车头在 处时,恰好位于 处的北偏东 方向上,10秒钟后,动车车头到达 处,恰好位于 处西北方向上,则这时段动车的平均速度是( )米/秒. A、 B、 C、200 D、30012. 已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10 km,一艘货轮从B港口沿如图所示的BC方向航行4 km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
A、 B、 C、200 D、30012. 已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10 km,一艘货轮从B港口沿如图所示的BC方向航行4 km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km. A、8 B、9 C、6 D、7
A、8 B、9 C、6 D、7二、填空题
-
13. 如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角 ,两树间的坡面距离 ,则这两棵树的水平距离约为m(结果精确到 ,参考数据: ).
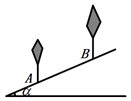 14. 如图,我市在建高铁的某段路基横断面为梯形 , ∥ , 长为6米,坡角 为45°, 的坡角 为30°,则 的长为 米 (结果保留根号)
14. 如图,我市在建高铁的某段路基横断面为梯形 , ∥ , 长为6米,坡角 为45°, 的坡角 为30°,则 的长为 米 (结果保留根号)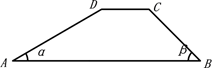 15. 如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为12.17米.从点A处测得桥墩顶部点C的仰角为 ,则AC的长为米(用三角函数表示).
15. 如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为12.17米.从点A处测得桥墩顶部点C的仰角为 ,则AC的长为米(用三角函数表示). 16. 观光塔是某市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°。已知楼房高AB是45m,根据以上观测数据可求观光塔的高CD是m。
16. 观光塔是某市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°。已知楼房高AB是45m,根据以上观测数据可求观光塔的高CD是m。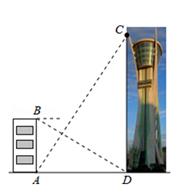 17. 如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60°,当他在B时测量该树的影长时,日照的光线与地面的夹角是30°,若两次测得的影长之差 为 ,则树的高度为 .(结果精确到0.1,参考数据: )
17. 如图,小军在A时测量某树的影长时,日照的光线与地面的夹角恰好是60°,当他在B时测量该树的影长时,日照的光线与地面的夹角是30°,若两次测得的影长之差 为 ,则树的高度为 .(结果精确到0.1,参考数据: ) 18. 如图,从甲楼顶部A处测得乙楼顶部D处的俯角α为30°,又从A处测得乙楼底部C处的俯角β为60°,已知两楼之间的距离BC为18米,则乙楼CD的高度为米。(结果保留根号)
18. 如图,从甲楼顶部A处测得乙楼顶部D处的俯角α为30°,又从A处测得乙楼底部C处的俯角β为60°,已知两楼之间的距离BC为18米,则乙楼CD的高度为米。(结果保留根号) 19. 如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=(结果用根号表示).
19. 如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=(结果用根号表示). 20. 某型号飞机的机翼形状如图所示,根据图中数据计算 的长为 .(结果保留根号)
20. 某型号飞机的机翼形状如图所示,根据图中数据计算 的长为 .(结果保留根号)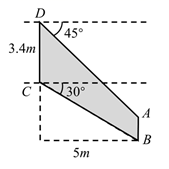
三、解答题
-
21. 为保障师生复学复课安全,某校利用热成像体温检测系统,对入校师生进行体温检测.如图是测温通道示意图,在测温通道侧面A点测得∠DAB=49°,∠CAB=35°.若AB=3m,求显示牌的高度DC.(sin35°≈0.57,tan35°≈0.70,sin49°=0.75,tan49°≈1.15,结果精确到0.1m).
 22. 两地间有一段笔直的高速铁路,长度为 .某时发生的地震对地面上以点C为圆心, 为半径的圆形区域内的建筑物有影响.分别从 两地处测得点C的方位角如图所示, .高速铁路是否会受到地震的影响.请通过计算说明理由.
22. 两地间有一段笔直的高速铁路,长度为 .某时发生的地震对地面上以点C为圆心, 为半径的圆形区域内的建筑物有影响.分别从 两地处测得点C的方位角如图所示, .高速铁路是否会受到地震的影响.请通过计算说明理由.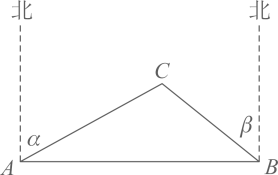 23. 在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D , 点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
23. 在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践,如图为实践时绘制的截面图.无人机从地面点B垂直起飞到达点A处,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D , 点B为CD的中点,求2号楼的高度.(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)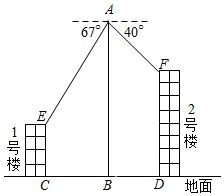 24. 如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点 处测得码头 的船的东北方向,航行40分钟后到达 处,这时码头 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头 的最近距离.(结果精确的0.1海里,参考数据 )
24. 如图,一艘船以每小时30海里的速度向北偏东75°方向航行,在点 处测得码头 的船的东北方向,航行40分钟后到达 处,这时码头 恰好在船的正北方向,在船不改变航向的情况下,求出船在航行过程中与码头 的最近距离.(结果精确的0.1海里,参考数据 )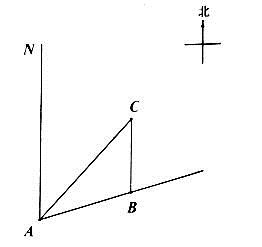 25. 如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m , 为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E , 测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E , 测得仰角为45°,求该电视塔的高度EF .
25. 如图,甲楼AB高20米,乙楼CD高10米,两栋楼之间的水平距离BD=30m , 为了测量某电视塔EF的高度,小明在甲楼楼顶A处观测电视塔塔顶E , 测得仰角为37°,小明在乙楼楼顶C处观测电视塔塔顶E , 测得仰角为45°,求该电视塔的高度EF .(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, )
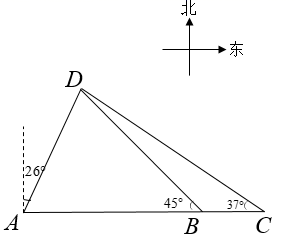
 26. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )
26. 如图,在港口A处的正东方向有两个相距 的观测点B、C,一艘轮船从A处出发, 北偏东 方向航行至D处, 在B、C处分别测得 , 求轮船航行的距离AD (参考数据: , , , , , )