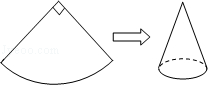
初中数学苏科版九年级上册2.8 圆锥的侧面积 同步测试
试卷更新日期：2020-09-02 类型：同步测试
一、单选题
-
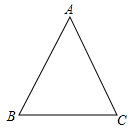
1. 已知圆锥的底面半径为 ，母线长为 ，则圆锥的侧面积是（ ）A、 B、 C、 D、2. 如图，△ABC是一圆锥的主视图.若AB=AC=60，BC=50，则该圆锥的侧面积为（ ）
A、1500π B、3000π C、750π D、2000π3. 用一个半径为 面积为 的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径为（ ）A、 B、 C、2 D、14. 一个圆锥的底面半径r＝10，高h＝20，则这个圆锥的侧面积是（ ）A、100 π B、200 π C、100 π D、200 π5. 如图，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径 ，高 ，则这个零件的表面积是（ ）
A、 B、 C、 D、6. 如图，蒙古包可近似看作由圆锥和圆柱组成，若用毛毡搭建一个底面圆面积为25πm2 ， 圆柱高为3m，圆锥高为2m的蒙古包，则需要毛毡的面积是（ ）
A、(30+5 )πm2 B、40πm2 C、(30+5 )πm2 D、55πm27. 一个圆锥的侧面积是底面积的4倍，则圆锥侧面展开图的扇形的圆心角是（ ）A、60° B、90° C、120° D、180°8. 已知圆锥的高为 ，母线为 ，且 ，圆锥的侧面展开图为如图所示的扇形．将扇形沿 折叠，使A点恰好落在 上的F点，则弧长 与圆锥的底面周长的比值为（ ）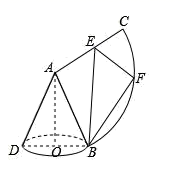
A、 B、 C、 D、二、填空题
-
9. 若圆锥的底面周长为 ，母线长为6，则圆锥的侧面积等于.（结果保留π）10. 一个圆锥的底面半径为3，高为4，则此圆锥的侧面积为.11. 圆锥的底面半径为3，侧面积为 ，则这个圆锥的母线长为.12. 用半径为30，圆周角为120°的扇形纸片围成一个圆锥的侧面，那么这个圆锥的底面圆半径是.
13. 用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.14. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形.若圆锥的母线长l为6cm，扇形的圆心角θ＝120°，则该圆锥的侧面积为cm2.（结果保留π）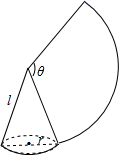
15. 如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体展开图的圆心角是.
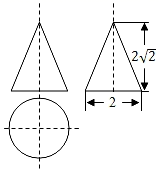16. 已知圆锥的底面圆的半径是2.5，母线长是9，其侧面展开图的圆心角是度．17. 如图所示，小明从半径为 的圆形纸片中剪下 圆周的一个扇形，然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠)，那么这个圆锥的高为（ ）
A、 B、 C、 D、18. 已知圆锥的高为 ，高所在的直线与母线的夹角为 ，则圆锥的侧面积为A、 B、 C、 D、三、解答题
-
19. 如图，用一张长为2π米、宽为2米的铁皮制作一个圆柱形管道，如果制作中不考虑材料损耗，试求可围成管道的最大体积.
