四川省成都市简阳市镇金学区、简城学区2019-2020学年九年级上学期数学12月月考试卷
试卷更新日期:2020-09-01 类型:月考试卷
一、单选题
-
1. 的相反数是( )A、 B、﹣ C、8 D、﹣82. 如图所示,该几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 地球与太阳的距离约为1.5亿千米,用科学记数法表示为( )A、1.5×10 千米 B、1.5×10 千米 C、1.5×10 千米 D、1.5×10 千米4. 在平面直角坐标系中,点A与点B关于x轴对称,若点A的坐标为(2,3),则点B所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,AB∥CD , 直线l交AB于点E , 交CD于F点,若∠1=70°,则∠2的度数为( )
3. 地球与太阳的距离约为1.5亿千米,用科学记数法表示为( )A、1.5×10 千米 B、1.5×10 千米 C、1.5×10 千米 D、1.5×10 千米4. 在平面直角坐标系中,点A与点B关于x轴对称,若点A的坐标为(2,3),则点B所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,AB∥CD , 直线l交AB于点E , 交CD于F点,若∠1=70°,则∠2的度数为( ) A、20° B、70° C、110° D、160°6. 下列各式计算正确的是( )A、a2+a2=a4 B、(﹣2x)3=﹣8x3 C、a3•a4=a12 D、(x﹣3)2=x2﹣97. 下列对一元二次方程x2+x﹣3=0根的情况的判断,正确的是( )A、有两个不相等实数根 B、有两个相等实数根 C、有且只有一个实数根 D、没有实数根8. 根据PM2.5空气质量标准:24小时PM2.5均值在0∽35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表,这组PM2.5数据的中位数是( )
A、20° B、70° C、110° D、160°6. 下列各式计算正确的是( )A、a2+a2=a4 B、(﹣2x)3=﹣8x3 C、a3•a4=a12 D、(x﹣3)2=x2﹣97. 下列对一元二次方程x2+x﹣3=0根的情况的判断,正确的是( )A、有两个不相等实数根 B、有两个相等实数根 C、有且只有一个实数根 D、没有实数根8. 根据PM2.5空气质量标准:24小时PM2.5均值在0∽35(微克/立方米)的空气质量等级为优.将环保部门对我市PM2.5一周的检测数据制作成如下统计表,这组PM2.5数据的中位数是( ) A、21微克/立方米 B、20微克/立方米 C、19微克/立方米 D、18微克/立方米9. 下列各组图形一定相似的是( )A、两个矩形 B、两个等边三角形 C、有一内角是80°的两个等腰三角形 D、两个菱形10. 当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )A、
A、21微克/立方米 B、20微克/立方米 C、19微克/立方米 D、18微克/立方米9. 下列各组图形一定相似的是( )A、两个矩形 B、两个等边三角形 C、有一内角是80°的两个等腰三角形 D、两个菱形10. 当k>0时,反比例函数y= 和一次函数y=kx+2的图象大致是( )A、 B、
B、 C、
C、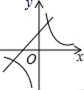 D、
D、
二、填空题
-
11. 函数y= 中,自变量x的取值范围是 .12. 菱形ABCD中,∠A:∠B=1:5,若周长为8,则此菱形的高等于 .13. 如图,点P在反比例函数y= (x<0)的图象上,过P作x轴,y轴的垂线,垂足分别为点A , B , 已知矩形PAOB的面积为3,则k= .
 14. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于 BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为 .
14. 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于 BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为 . 15. 若 (b+3d﹣f≠0),则 = .16. 在一个不透明的盒子中装有x颗白色棋子和y颗黑色棋子,它们除颜色外完全相同,现从该盒子总随机取出一颗棋子,取得白色棋子的概率是 ,将取出的棋子放回,再往该盒子中放进6颗同样的黑色棋子,此时从盒子中随机取出一颗棋子,取得白色棋子的概率是 ,那么原来盒子中的白色棋子有颗.17. 已知关于x的方程x2﹣(2k2﹣3)x+k+7=0的两个不等实数根x1、x2满足:x1=5﹣x2 , 则k的值为 .18. 对于一切不小于2的自然数n,关于x的一元二次方程x2﹣(n+2)x﹣2n2=0的两个根记作an , bn(n≥2), = .19. 如图,在边长为5的正方形ABCD中,点E在BC边上,连接AE,过D作DF//AE交BC的延长线于点F,过点C作CG⊥DF于点G,延长AE、GC交于点H,点P是线段DG上的任意一点(不与点D、点G重合),连接CP,将△CPG沿CP翻折得到 ,连接 . 若CH=1,则 长度的最小值为.
15. 若 (b+3d﹣f≠0),则 = .16. 在一个不透明的盒子中装有x颗白色棋子和y颗黑色棋子,它们除颜色外完全相同,现从该盒子总随机取出一颗棋子,取得白色棋子的概率是 ,将取出的棋子放回,再往该盒子中放进6颗同样的黑色棋子,此时从盒子中随机取出一颗棋子,取得白色棋子的概率是 ,那么原来盒子中的白色棋子有颗.17. 已知关于x的方程x2﹣(2k2﹣3)x+k+7=0的两个不等实数根x1、x2满足:x1=5﹣x2 , 则k的值为 .18. 对于一切不小于2的自然数n,关于x的一元二次方程x2﹣(n+2)x﹣2n2=0的两个根记作an , bn(n≥2), = .19. 如图,在边长为5的正方形ABCD中,点E在BC边上,连接AE,过D作DF//AE交BC的延长线于点F,过点C作CG⊥DF于点G,延长AE、GC交于点H,点P是线段DG上的任意一点(不与点D、点G重合),连接CP,将△CPG沿CP翻折得到 ,连接 . 若CH=1,则 长度的最小值为.
三、解答题
-
20.(1)、计算:(2)、解方程:21. 先化简,再求值:( + )÷ ,且x为满足﹣3<x<2的整数.22. 某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好(每人只能选其中一项),并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
 (1)、在这次考察中一共调查了名学生,请补全条形统计图;(2)、被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.23. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.求证:AE=CF.
(1)、在这次考察中一共调查了名学生,请补全条形统计图;(2)、被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.23. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.求证:AE=CF.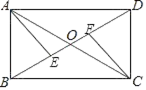 24. 如图,一次函数y=x+m的图象与反比例函数y= 的图象交于A , B两点,且与x轴交于点C , 点A的坐标为(2,1).
24. 如图,一次函数y=x+m的图象与反比例函数y= 的图象交于A , B两点,且与x轴交于点C , 点A的坐标为(2,1). (1)、求一次函数和反比例函数的解析式;(2)、求点C的坐标;(3)、结合图象直接写出不等式0<x+m≤ 的解集.25. 如图所示,在△ABC中,BA=BC=20cm , AC=30cm , 点P从A点出发沿AB方向以4cm/s的速度向B点运动,同时点Q从C点出发沿CA方向以3cm/s的速度向A点运动,设运动时间为xs .
(1)、求一次函数和反比例函数的解析式;(2)、求点C的坐标;(3)、结合图象直接写出不等式0<x+m≤ 的解集.25. 如图所示,在△ABC中,BA=BC=20cm , AC=30cm , 点P从A点出发沿AB方向以4cm/s的速度向B点运动,同时点Q从C点出发沿CA方向以3cm/s的速度向A点运动,设运动时间为xs . (1)、当x= 时,求 ;(2)、△APQ能否与△CQB相似?若能,求出AP的长;若不能,请说明理由.26. 某超市欲购进一种今年新上市的产品,购进价为20元/件,该超市进行了试销售,得知该产品每天的销售量t(件)与每件销售价x(元/件)之间有如下关系: .(1)、请写出该超市销售这种产品每天的销售利润y(元)与x之间的函数表达式;(2)、当x为多少元时,销售利润最大?最大利润是多少?27. 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E , 交BC边于F , 分别连结AF和CE .
(1)、当x= 时,求 ;(2)、△APQ能否与△CQB相似?若能,求出AP的长;若不能,请说明理由.26. 某超市欲购进一种今年新上市的产品,购进价为20元/件,该超市进行了试销售,得知该产品每天的销售量t(件)与每件销售价x(元/件)之间有如下关系: .(1)、请写出该超市销售这种产品每天的销售利润y(元)与x之间的函数表达式;(2)、当x为多少元时,销售利润最大?最大利润是多少?27. 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E , 交BC边于F , 分别连结AF和CE . (1)、求证:四边形AFCE是菱形;(2)、若AE=13cm , △ABF的周长为30cm , 求△ABF的面积;(3)、在线段AC上是否存在一点P , 使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.28. 如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)、求证:四边形AFCE是菱形;(2)、若AE=13cm , △ABF的周长为30cm , 求△ABF的面积;(3)、在线段AC上是否存在一点P , 使得2AE2=AC•AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.28. 如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB. (1)、直接写出BC的长是 , 点D的坐标是;(2)、证明:△AEF与△DCE相似;(3)、当△EFC为等腰三角形时,求点E的坐标.
(1)、直接写出BC的长是 , 点D的坐标是;(2)、证明:△AEF与△DCE相似;(3)、当△EFC为等腰三角形时,求点E的坐标.