山东省泰安市泰山区2019-2020学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-09-01 类型:期中考试
一、单选题
-
1. 等于( )A、 B、 C、 D、2. 下列函数:① ;② ;③ ;④ ;⑤ .反比例函数有( )A、 个 B、 个 C、 个 D、 个3. 如图,在平面直角坐标系中,点 的坐标为 ,那么 的值是( )
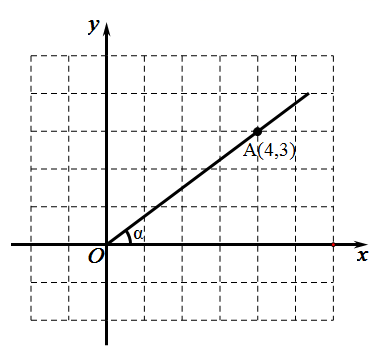 A、 B、 C、 D、4. 二次函数 的图象向左平移2个单位,得到新的图象的函数表达式是( )A、 B、 C、 D、5. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )A、y= B、y= C、y= D、y=6. 如图,某水库堤坝横断面迎水坡AB的坡比是1: ,堤坝高BC=50m,则应水坡面AB的长度是( )
A、 B、 C、 D、4. 二次函数 的图象向左平移2个单位,得到新的图象的函数表达式是( )A、 B、 C、 D、5. 近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜镜片的焦距为0.25m,则y与x的函数关系式为( )A、y= B、y= C、y= D、y=6. 如图,某水库堤坝横断面迎水坡AB的坡比是1: ,堤坝高BC=50m,则应水坡面AB的长度是( )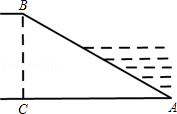 A、100m B、100 m C、150m D、50 m7. 一次函数y=ax+a(a为常数,a≠0)与反比例函数y= (a为常数,a≠0)在同一平面直角坐标系内的图像大致为( )A、
A、100m B、100 m C、150m D、50 m7. 一次函数y=ax+a(a为常数,a≠0)与反比例函数y= (a为常数,a≠0)在同一平面直角坐标系内的图像大致为( )A、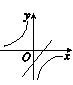 B、
B、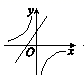 C、
C、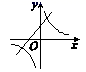 D、
D、 8. 已知二次函数 ,若自变量x分别取 , , ,且 ,则对应的函数值 , , 的大小关系正确的是( )A、 B、 C、 D、9. 若抛物线 经过点 ,则 的值是( )A、6 B、7 C、8 D、2010. a,b是实数,点 、 在反比例函数 的图像上,则( )A、 B、 C、 D、11. 如图,A、B两点在双曲线 上,分别经过A、B两点向坐标轴作垂线段,已知 ,则 ( )
8. 已知二次函数 ,若自变量x分别取 , , ,且 ,则对应的函数值 , , 的大小关系正确的是( )A、 B、 C、 D、9. 若抛物线 经过点 ,则 的值是( )A、6 B、7 C、8 D、2010. a,b是实数,点 、 在反比例函数 的图像上,则( )A、 B、 C、 D、11. 如图,A、B两点在双曲线 上,分别经过A、B两点向坐标轴作垂线段,已知 ,则 ( )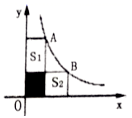 A、 B、 C、 D、12. 对于函数 的图象,下列说法错误的是( )A、开口向下 B、对称轴是直线 C、最大值为k D、与y轴不相交13. 若函数 的图象与坐标轴有三个交点,则 的取值范围是( )
A、 B、 C、 D、12. 对于函数 的图象,下列说法错误的是( )A、开口向下 B、对称轴是直线 C、最大值为k D、与y轴不相交13. 若函数 的图象与坐标轴有三个交点,则 的取值范围是( )
A、 B、 C、 D、14. 已知抛物线 的对称轴为直线 ,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论:①抛物线过点 ;② ;③ ;④抛物线的顶点坐标为 ;⑤当 时,y随x增大而增大.其中结论错误的是( )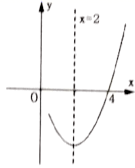 A、②③④ B、②③⑤ C、③⑤ D、③④⑤
A、②③④ B、②③⑤ C、③⑤ D、③④⑤二、填空题
-
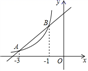
15. 反比例函数 的图象在一、三象限,则k应满足.16. 中, , ,则 .17. 如图,反比例函数 与一次函数y=x+4的图象交于A、B两点的横坐标分别为-3,-1,则关于x的不等式 的解集为.
 18. 如图,从热气球C处测得地面A、B两点的俯角分别为 、 ,如果此时热气球C处的高度 为 米,点A、D、B在同一直线上,则 两点的距离是米.(保留根号)
18. 如图,从热气球C处测得地面A、B两点的俯角分别为 、 ,如果此时热气球C处的高度 为 米,点A、D、B在同一直线上,则 两点的距离是米.(保留根号)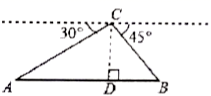 19. 若抛物线 与x轴没有交点,则m的取值范围是 .20. 飞机着陆后滑行的距离 单位:米 关于滑行的时间 单位:秒 的函数解析式是 ,则飞机着陆后滑行的最长时间为 秒21. 如图,正方形 的边长为1, 边在x轴负半轴上,反比例函数 的图象经过点B和 边中点E,则k的值为 .
19. 若抛物线 与x轴没有交点,则m的取值范围是 .20. 飞机着陆后滑行的距离 单位:米 关于滑行的时间 单位:秒 的函数解析式是 ,则飞机着陆后滑行的最长时间为 秒21. 如图,正方形 的边长为1, 边在x轴负半轴上,反比例函数 的图象经过点B和 边中点E,则k的值为 .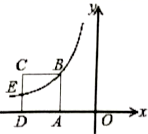 22. 已知二次函数 自变量x的部分取值和对应函数值y如下表:
22. 已知二次函数 自变量x的部分取值和对应函数值y如下表:…
-2
-1
0
1
2
3
…
…
5
0
-3
-4
-3
0
…
则在实数范围内能使 成立的x的取值范围是.
三、解答题
-
23. 如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数 的图象于点B,AB= .
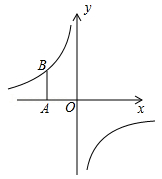 (1)、求反比例函数的解析式;(2)、若P( , )、Q( , )是该反比例函数图象上的两点,且 时, ,指出点P、Q各位于哪个象限?并简要说明理由.
(1)、求反比例函数的解析式;(2)、若P( , )、Q( , )是该反比例函数图象上的两点,且 时, ,指出点P、Q各位于哪个象限?并简要说明理由.
24. 某太阳能热水器的横截面示意图如图所示。已知真空热水管 与支架 所在直线相交于点O,且 ,支架 与水平线 垂直, , , .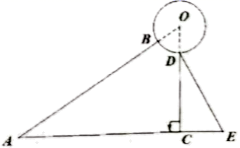 (1)、求支架 的长;(2)、求真空热水管 的长.(结果均保留根号).25. 在所给的平面直角坐标系中画出函数 的图象,利用图象回答:
(1)、求支架 的长;(2)、求真空热水管 的长.(结果均保留根号).25. 在所给的平面直角坐标系中画出函数 的图象,利用图象回答: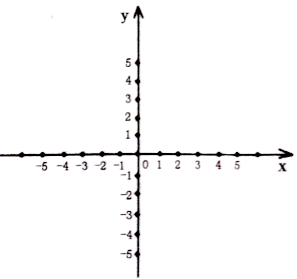 (1)、画图。(2)、方程 的解是什么?(3)、x取什么值时,函数值小于0?(4)、x取什么值时,函数值大于5?26. 如图,一次函数y=kx+b与反比例函数y= 的图象交于A(2,3),B(﹣3,n)两点.
(1)、画图。(2)、方程 的解是什么?(3)、x取什么值时,函数值小于0?(4)、x取什么值时,函数值大于5?26. 如图,一次函数y=kx+b与反比例函数y= 的图象交于A(2,3),B(﹣3,n)两点.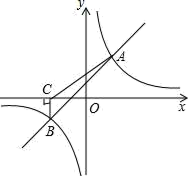 (1)、求一次函数与反比例函数的解析式;(2)、过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.27. 某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
(1)、求一次函数与反比例函数的解析式;(2)、过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.27. 某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.设每个房间每天的定价增加x元.求:
(1)、房间每天的入住量y(间)关于x(元)的函数关系式;(2)、该宾馆每天的房间收费p(元)关于x(元)的函数关系式;(3)、该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?28. 如图,二次函数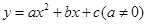 的图象交x轴于
的图象交x轴于  两点,交y轴于点D,点B的坐标为
两点,交y轴于点D,点B的坐标为 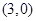 ,顶点C的坐标为
,顶点C的坐标为 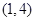 .
. 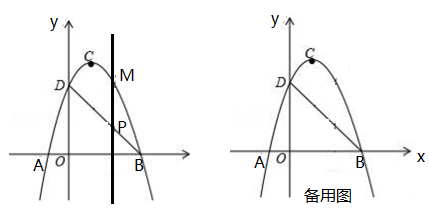 (1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q,使
(1)、求二次函数的解析式和直线BD的解析式;(2)、点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;(3)、在抛物线上是否存在异于B、D的点Q,使 中BD边上的高为
中BD边上的高为 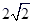 ,若存在求出点Q的坐标;若不存在请说明理由.
,若存在求出点Q的坐标;若不存在请说明理由.