四川省绵阳市涪城区2019-2020学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-09-01 类型:月考试卷
一、单选题
-
1. 若 ,则 ( )A、 B、 C、-2或2 D、2. 如图 与 相切于点 为 上点,则下列说法中错误的( )
 A、 是圆心角 B、 是圆周角 C、 是圆周角 D、 是圆心角3. 下列对于抛物线 的描述错误的是( )A、开口向下 B、对称轴是 C、与 轴交于 D、顶点是4. 绵阳城市形象标识今年正式发布,其图案如下图,图案由四部分构成,其中是中心对称图形的有( )部分
A、 是圆心角 B、 是圆周角 C、 是圆周角 D、 是圆心角3. 下列对于抛物线 的描述错误的是( )A、开口向下 B、对称轴是 C、与 轴交于 D、顶点是4. 绵阳城市形象标识今年正式发布,其图案如下图,图案由四部分构成,其中是中心对称图形的有( )部分 A、1 B、2 C、3 D、45. 如图, 是 的直径, 是 的弦,如果 ,那么 ( )
A、1 B、2 C、3 D、45. 如图, 是 的直径, 是 的弦,如果 ,那么 ( ) A、 B、 C、 D、6. 如果关于x的一元二次方程 有实数根,那么m的取值范围是( )A、 B、 C、 D、7. 在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加美感,按此比例,如果雕像的身高为3米,设雕像的上部为x米,根据其比例关系可得其方程应为( )A、 B、 C、 D、8. 如图将 绕点A逆时针旋转 得到相应的 若点D恰在线段 的延长线上,则下列选项中错误的是( )
A、 B、 C、 D、6. 如果关于x的一元二次方程 有实数根,那么m的取值范围是( )A、 B、 C、 D、7. 在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加美感,按此比例,如果雕像的身高为3米,设雕像的上部为x米,根据其比例关系可得其方程应为( )A、 B、 C、 D、8. 如图将 绕点A逆时针旋转 得到相应的 若点D恰在线段 的延长线上,则下列选项中错误的是( ) A、 B、 C、 D、9. 已知x是方程 的根,那么代数式 的值是( )A、 B、 C、 D、10. 若点 是抛物线 上的点,则 的最小值是( )A、 B、 C、 D、11. 如图,抛物线 与直线 交于 两点,点C为y轴上点,当 周长最短时;周长的值为( )
A、 B、 C、 D、9. 已知x是方程 的根,那么代数式 的值是( )A、 B、 C、 D、10. 若点 是抛物线 上的点,则 的最小值是( )A、 B、 C、 D、11. 如图,抛物线 与直线 交于 两点,点C为y轴上点,当 周长最短时;周长的值为( ) A、 B、 C、 D、12. 如图,在平面直角坐标系 中 ,若在直线 上存在点 满足 ,则 的取值范围是( )
A、 B、 C、 D、12. 如图,在平面直角坐标系 中 ,若在直线 上存在点 满足 ,则 的取值范围是( )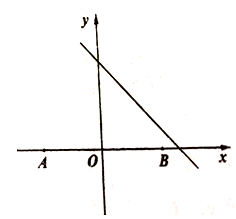 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式:1﹣x2= .14. 将抛物线 向左平移 个单位,再向上平移 个单位后新的抛物线的顶点坐标是 .15. 在圆中,直径 为圆上点,且 ,若如图分布的6个圆心在 上且大小相等的小圆均与 相切,则CD= .
 16. 已知抛物线 的对称轴是 ,若关于x的方程 的一个根是4,那么该方程的另一个根是 .17. 如图 中, ,以 为直径的 与 交于点D,若E为 的中点,则
16. 已知抛物线 的对称轴是 ,若关于x的方程 的一个根是4,那么该方程的另一个根是 .17. 如图 中, ,以 为直径的 与 交于点D,若E为 的中点,则 18. 如图为二次函数 图象,直线 与抛物线交于 两点, 两点横坐标分别为 根据函数图象信息有下列结论:
18. 如图为二次函数 图象,直线 与抛物线交于 两点, 两点横坐标分别为 根据函数图象信息有下列结论:① ;
②若对于 的任意值都有 ,则 ;
③ ;
④ ;
⑤当t为定值时若a变大,则线段 变长
其中,正确的结论有(写出所有正确结论的番号)

三、解答题
-
19. 解下列方程:(1)、(2)、20. 已知关于x的方程(1)、若方程有两相等实数根,求m的取值;(2)、若方程其中-根为 ,求其另一根及m的值.21. 如图在平面直角坐标系 中, ,将 绕点O逆时针旋转 后得到
 (1)、填空:(2)、求 的坐标;(3)、求 的坐标.22. 生产商对在甲、乙两地生产并销售的某产品进行研究后发现如下规律:每年年产量为x(吨)时所需的全部费用y(万元)与x满足关系式 ,投人市场后当年能全部售10出,且在甲、乙两地每吨的售价 (万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)(1)、当在甲地生产并销售x吨时,满足 ,求在甲地生成并销售20吨时利润为多少万元;(2)、当在乙地生产并销售x吨时, ,求在乙地当年的最大年利润应为多少万元?23. 如图, 在 上, 经过圆心O的线段 于点F,与 交于点E.
(1)、填空:(2)、求 的坐标;(3)、求 的坐标.22. 生产商对在甲、乙两地生产并销售的某产品进行研究后发现如下规律:每年年产量为x(吨)时所需的全部费用y(万元)与x满足关系式 ,投人市场后当年能全部售10出,且在甲、乙两地每吨的售价 (万元)均与x满足一次函数关系.(注:年利润=年销售额-全部费用)(1)、当在甲地生产并销售x吨时,满足 ,求在甲地生成并销售20吨时利润为多少万元;(2)、当在乙地生产并销售x吨时, ,求在乙地当年的最大年利润应为多少万元?23. 如图, 在 上, 经过圆心O的线段 于点F,与 交于点E. (1)、如图1,当 半径为 ,若 ,求弦 的长;(2)、如图2,当 半径为 , ,若 ,求弦 的长.
(1)、如图1,当 半径为 ,若 ,求弦 的长;(2)、如图2,当 半径为 , ,若 ,求弦 的长.

