山东省菏泽市东明县2019-2020学年九年级上学期数学10月月考试卷

试卷更新日期：2020-09-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程中，关于x的一元二次方程是（）

A、3(x＋1)²＝2(x＋1) B、 $\frac{1}{x^{2}}$ ＋ $\frac{1}{x}$ －2＝0 C、ax²＋bx＋c＝0 D、x²＋2x＝x²－1

查看试题解析
2. 如图，已知四边形ABCD是平行四边形，下列结论中错误的是（）

A、当AB=BC时，四边形ABCD是菱形 B、当AC⊥BD时，四边形ABCD是菱形 C、当∠ABC=90°时，四边形ABCD是矩形 D、当AC=BD时，四边形ABCD是正方形

查看试题解析
3. 抛掷一个质地均匀的正方体玩具（它的每个面上分别标有数字1，2，3，4，5，6），它落地时向上的数是3的概率是（　　）

A、 $\frac{1}{3}$ B、1 C、 $\frac{1}{2}$ D、 $\frac{1}{6}$

查看试题解析
4.
如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为（　　）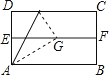

A、30° B、45° C、60° D、75°

查看试题解析
5. 如图，菱形ABCD中，AB=4，∠B=60°，AE⊥BC，AF⊥CD，垂足分别为E，F，连接EF，则△AEF的面积是（）

A、4 $\sqrt{3}$ B、3 $\sqrt{3}$ C、2 $\sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
6. 若一元二次方程2x（kx﹣4）﹣x²+6=0无实数根，则k的最小整数值是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
7. 用配方法解一元二次方程 $x^{2} - 4 x = 5$ 时，此方程可变形为（）

A、 ${(x + 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 1$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
8. 下列说法错误的是（）

A、某事件发生的概率为1，则它必然会发生 B、某事件发生的概率为0，则它必然不会发生 C、抛一个普通纸杯，杯口不可能向上 D、从一批产品中任取一个为次品是可能的

查看试题解析
9. 下列条件之一能使菱形ABCD是正方形的为（　　）
①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD．

A、①③ B、②③ C、②④ D、①②③

查看试题解析
10. 已知关于x的一元二次方程x²+ax+b=0有一个非零根﹣b，则a﹣b的值为（）

A、1 B、﹣1 C、0 D、﹣2

查看试题解析
11. 用一条长为40cm的绳子围成一个面积为acm²的长方形，a的值不可能为（）

A、20 B、40 C、100 D、120

查看试题解析
12. 如图，正方形ABCD的边长为4，点E在对角线BD上，且 $∠ BAE ＝ 22 . 5^{0}$ ，EF⊥AB，垂足为F，则EF的长为（）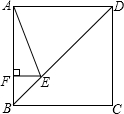

A、1 B、 $\sqrt{2}$ C、 $4 - 2 \sqrt{2}$ D、 $3 \sqrt{2} - 4$

查看试题解析

二、填空题

13. 一元二次方程2x²＋6x＝9的二次项系数、一次项系数、常数项和为．

查看试题解析
14. 去掉大小王一副牌共52张，任取两张，则两张为同色的概率等于．

查看试题解析
15. 如图，矩形ABCD中，AB=1，E、F分别为AD、CD的中点，沿BE将△ABE折叠，若点A恰好落在BF上，则AD= ．

查看试题解析
16.
如图，在矩形ABCD中，点E、F分别在边CD、BC上，且DC=3DE=3a．将矩形沿直线EF折叠，使点C恰好落在AD边上的点P处，则FP= ．

查看试题解析

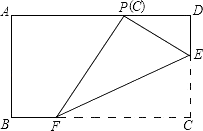
三、解答题

17. 解方程：

(1)、x²－4x＋2＝0; 　　　

(2)、x²＋3x＋2＝0；

(3)、3x²－7x＋4＝0.

查看试题解析
18. 某校八年级将举行班级乒乓球对抗赛，每个班必须选派出一对男女混合双打选手参赛．八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中，选男、女选手各一名组成一对选手参赛，一共能够组成哪几对？如果小敏和小强的组合是最强组合，那么采用随机抽签的办法，恰好选出小敏和小强参赛的概率是多少？

查看试题解析
19. 如图，利用一面墙(墙EF最长可利用28米)，围成一个矩形花园ABCD．与墙平行的一边BC上要预留2米宽的入口(如图中MN所示，不用砌墙)．现有砌60米长的墙的材料．

(1)、当矩形的长BC为多少米时，矩形花园的面积为300平方米；

(2)、能否围成480平方米的矩形花园，为什么？

查看试题解析
20. 如图，已知△ABC中，∠ACB=90°，CE是中线，△ACD与△ACE关于直线AC对称．

(1)、求证：四边形ADCE是菱形；

(2)、求证：BC=ED ．

查看试题解析
21. 李明准备进行如下操作实验，把一根长40 cm的铁丝剪成两段，并把每段首尾相连各围成一个正方形．

(1)、要使这两个正方形的面积之和等于58 cm² ，李明应该怎么剪这根铁丝？

(2)、李明认为这两个正方形的面积之和不可能等于48 cm² ，你认为他的说法正确吗？请说明理由．

查看试题解析
22. 如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC ．设MN交∠ACB的平分线于点E ，交∠ACB的外角平分线于点F ．

(1)、求证：OE＝OF；

(2)、若CE＝8，CF＝6，求OC的长；

(3)、当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

查看试题解析