广西北海市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-01 类型：期末考试

进入 出卷网 下载

一、选择题（每小题3分，共30分）

  • 1. 下列图形中，为中心对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 下列函数中，不是一次函数的是（   ）
    A、y＝x+4 B、y＝ 25 x C、y＝2﹣3x D、y＝ 7x

    查看试题解析

  • 3. 某校对1500名学生的视力进行了检查，其值在5.0～5.1这一小组的频率为0.30，则该组的人数为（   ）
    A、150人 B、450人 C、600人 D、1050人

    查看试题解析

  • 4. 下列四组线段中，能组成直角三角形的是（   ）
    A、a＝2，b＝3，c＝4 B、a＝3，b＝4，c＝5 C、a＝4，b＝5，c＝6 D、a＝7，b＝8，c＝9

    查看试题解析

  • 5. 如图，在四边形ABCD中，DE平分∠ADC交BC于点E，AF⊥DE，垂足为点F，若∠DAF＝50°，则∠EDC＝（   ）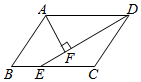

    A、40° B、50° C、80° D、100°

    查看试题解析

  • 6. 一次函数y=x+2的图象不经过（）

    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 7. 如图，在△ABC中，∠C＝90°，DE⊥AB于D，BC＝BD，如果AC＝3m，那么AE+DE等于（   ）

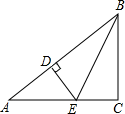    A、2.5m B、3m C、3.5m D、4m

    查看试题解析

  • 8. 如图，四边形ABCD是矩形，BC＝4cm，∠CBD：∠ABD＝2：1，则AC＝（   ）

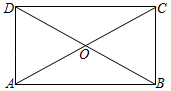    A、433 cm B、833 cm C、6cm D、8cm

    查看试题解析

  • 9. 如图，小明的父母出去散步，从家走了20分钟到一个离家900米的报亭，母亲随即按原速度返回家，父亲在报亭看了10分钟报纸后，用15分钟返回家，则分别表示父亲、母亲离家距离与时间之间关系的是（   ）

    A、①③ B、①② C、④② D、④③

    查看试题解析

  • 10. 正方形A1B1C1O，A2B2C2C1 ， A3B3C3C2 ， …按如图的方式放置，点A1 ， A2 ， A3 ， …和点C1 ， C2 ， C3 ， …分别在直线y＝x+1和x轴上，则点B6的纵坐标是（   ）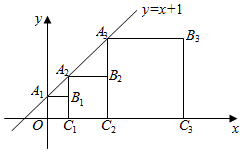

    A、8 B、32 C、64 D、126

    查看试题解析

二、填空题（每小题3分，共15分）

  • 11. 在平面直角坐标系中，点P（﹣3，4）关于x轴的对称点的坐标是.

    查看试题解析

  • 12. 点A（﹣1，y1），B（3，y2）是直线y＝3x﹣1上的两点，则y1y2.（填“＞”或“＜”）

    查看试题解析

  • 13. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为 ．

    查看试题解析

  • 14. 如图，菱形ABCD的两条对角线AC，BD相交于点O，E是AB的中点，若AC＝6，BD＝8，则OE的长为.

    查看试题解析

  • 15. 如图，在平面直角坐标系xOy中，一次函数y＝kx+b的图象经过A（﹣2，﹣2），B（1，4）两点，则△AOB的面积为.

    查看试题解析

三、解答题（共55分）

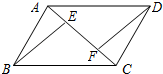
  • 16. 已知：如图，E，F是▱ABCD的对角线AC上两点，且AE＝CF.求证：BE＝DF.

    查看试题解析

  • 17. 已知y与x成正比例，且x＝2时，y＝4.
    (1)、求y关于x的函数表达式；
    (2)、当x＝﹣ 12 时，求y的值.

    查看试题解析

  • 18. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（2，﹣1），B（1，﹣2），C（3，﹣3）.

    (1)、△ABC的面积是.
    (2)、①将△ABC向上平移4个单位长度得到△A1B1C1 ， 请画出△A1B1C1；

    ②请画出与△ABC关于y轴对称的△A2B2C2.

    查看试题解析

  • 19. 某校七年级1班体育委员统计了全班同学60秒跳绳的次数，并绘制出如下频数分布表和频数分布直方图：

    次数

    80≤x＜100

    100≤x＜120

    120≤x＜140

    140≤x＜160

    160≤x＜180

    180≤x＜200

    频数

    a

    4

    12

    16

    8

    3

    结合图表完成下列问题：

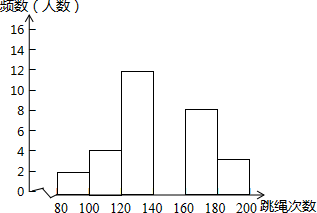    (1)、a＝；
    (2)、补全频数分布直方图；
    (3)、写出全班人数是 ， 并求出第三组“120≤x＜140”的频率（精确到0.01）
    (4)、若跳绳次数不少于140的学生成绩为优秀，则优秀学生人数占全班总人数的百分之几？

    查看试题解析

  • 20. 如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD、BE＝CF，

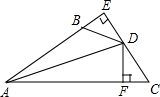    (1)、求证：AD平分∠BAC；
    (2)、已知AC＝20，BE＝4，求AB的长.

    查看试题解析

  • 21. 已知一个红外线测温仪售价380元，一包口罩售价40元，某学校准备购进红外线测温仪20个，口罩若干包（超过30包）.某药店对这两种商品给出优惠活动，活动一：购买1个红外线测温仪送1包口罩；活动二：购买口罩30包以上，超出30包的部分按售价的五折优惠，红外线测温仪不打折.
    (1)、设购买口罩x包，选择活动一的总费用为y1元，选择活动二的总费用为y2元，请分别求出y1 ， y2与x的函数关系式；
    (2)、学校购买口罩的包数x在什么范围内，选择优惠活动一比活动二更省钱？请说明理由.

    查看试题解析

  • 22. 如图，P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，点E，F分别是垂足.

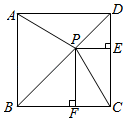    (1)、求证：AP＝PC；
    (2)、若∠BAP＝60°，PD＝ 2 ，求PC的长.

    查看试题解析

  • 23. 如图，在Rt△ABC中，∠B＝90°，AC＝40cm，∠A＝60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤10），过点D作DF⊥BC于点F，连接DE，EF．

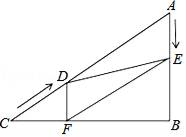    (1)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
    (2)、当t为何值时，△DEF为直角三角形？请说明理由．

    查看试题解析