陕西省宝鸡市陇县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-09-01 类型：期末考试

进入出卷网下载

一、选择题（每小题只有一个选项是符合题意的，每小题3分，共30分）

1. 如图，直线a，b被直线c所截，下列条件中，不能判定a∥b（）

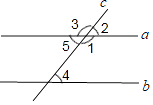A、∠2=∠4 B、∠1+∠4=180° C、∠5=∠4 D、∠1=∠3

查看试题解析
2. 某县共有1万名学生参加数学考试，现从中抽取600名考生的数学成绩进行统计分析，以下说法正确的是( ）

A、这是一次成绩普查 B、1万名考生是总体 C、每名考生的数学成绩是个体 D、600名考生是总体的一个样本

查看试题解析
3. 点A（x，y）的坐标满足xy＞0，x+y＜0，那么点A在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 用代入法解方程组 ${\begin{cases} y = 1 - x \\ x - 2 y = 4 \end{cases}$ 时，代入正确的是（）

A、x－2－x＝4 B、x－2－2x＝4 C、x－2＋2x＝4 D、x－2＋x＝4

查看试题解析
5. 如图，若“马”所在的位置的坐标为 $(- 2 ， 2)$ ，“象”所在位置的坐标为 $(- 1 ， 4)$ ，则“将”所在位置的坐标为（）

A、 $(4 ， 1)$ B、 $(1 ， 4)$ C、 $(1 ， 2)$ D、 $(2 ， 1)$

查看试题解析
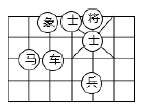6. 不等式组 ${\begin{cases} \frac{1}{2} x + 1 \geq - 3 \\ x - 2 (x - 3) > 0 \end{cases}$ 的最大整数解为（）

A、8 B、7 C、6 D、5

查看试题解析
7. 若点P（x，y）在第四象限，且|x|＝2，|y|＝3，则x+y＝（　　）

A、﹣1 B、1 C、5 D、﹣5

查看试题解析
8. 如图，AB∥CD，∠1＝45°，∠3＝80°，则∠2的度数为（）．

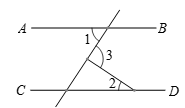A、30° B、35° C、40° D、45°

查看试题解析
9. 小明在解关于x，y的二元一次方程组 ${\begin{cases} x+ y = △ \\ 2 x-3y=5 \end{cases}$ 时，解得 ${\begin{cases} x=4 \\ y = \otimes \end{cases}$ ，则△和⊗代表的数分别是（）

A、△＝1，⊗＝5 B、△＝5，⊗＝1 C、△＝－1，⊗＝3 D、△＝3，⊗＝－1

查看试题解析
10. 老张从一个鱼摊上买了三条鱼，平均每条a元，又从另一个鱼摊上买了两条鱼，平均每条b元，后来他又以每条 $\frac{a + b}{2}$ 元的价格把鱼全部卖给了乙，结果发现赔了钱，原因是（）

A、a＞b B、a＜b C、a＝b D、与a和b的大小无关

查看试题解析

二、填空题（共4小题，每小题3分，计12分）

11. 一个正数的平方根为 $2 x + 1$ 和 $x - 7$ ，则这个正数为.

查看试题解析
12. 如图，OC是∠AOB的角平分线，l//OB，若∠1=52°，则∠2的度数为.

查看试题解析
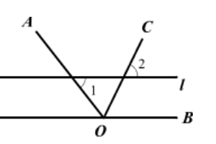13. 在平面直角坐标系中，A（－3，6），M是 x轴上一动点，当AM的值最小时，点M的坐标为．

查看试题解析
14. 若关于x的不等式组 ${\begin{cases} \frac{2 x + 5}{3} > x - 5 \\ \frac{x + 3}{2} < x + a \end{cases}$ 只有5个整数解，则a的取值范围

查看试题解析

三、解答题（共8小题，计55分）

15. 解方程组

(1)、 ${\begin{cases} 2 x - 3 y = 5 \\ 4 x - 5 y = 7 \end{cases}$

(2)、 ${\begin{cases} \frac{x + 3 y}{2} = \frac{3}{5} \\ 5 (x - 2 y) = - 4 \end{cases}$

查看试题解析
16. 解不等式组：并它的解集表示在数轴上．

(1)、 ${\begin{cases} 2 x - 1 > 3 ， ① \\ 2 + 2 x \geq 1 + x ， ② \end{cases}$

(2)、 ${\begin{cases} 2 (x + 2) \leq x + 3 ， ① \\ \frac{x}{3} < \frac{x + 1}{4} ， ② \end{cases}$

查看试题解析
17. 已知：如图，∠A＝∠ADE ， ∠C＝∠E ．

(1)、若∠EDC＝3∠C ，求∠C的度数；

(2)、求证：BE∥CD ．

查看试题解析
18. 已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′ ．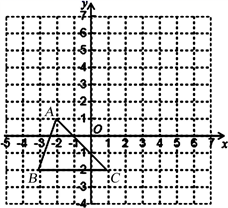

(1)、写出A′、B′、C′的坐标；

(2)、求出△ABC的面积；

(3)、点P在y轴上，且△BCP与△ABC的面积相等，求点P的坐标．

查看试题解析
19. 已知6是5a+6b的算术平方根，-2是a-4b-10的立方根，求a-2b的平方根．

查看试题解析
20. 如图，∠ADE+∠BCF＝180°，BE平分∠ABC，∠ABC＝2∠E．

(1)、AD与BC平行吗？请说明理由；

(2)、AB与EF的位置关系如何？为什么？

查看试题解析

21. 为了解同学们的身体发育情况，学校体卫办公室对七年级全体学生进行了身高测量（精确到1cm），并从中抽取了部分数据进行统计，请根据尚未完成的频数分布表和频数分布直方图解答下列问题：

频率分布表

分组	频数	百分比
144.5～149.5	2	4%
149.5～154.5	3	6%
154.5～159.5	a	16%
159.5～164.5	17	34%
164.5～169.5	b	n%
169.5～174.5	5	10%
174.5～179.5	3	6%

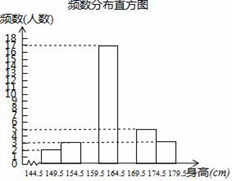(1)、求a、b、n的值；

(2)、补全频数分布直方图；

(3)、学校准备从七年级学生中选拔护旗手，要求身高不低于170cm，如果七年级有学生350人，护旗手的候选人大概有多少？

查看试题解析

22. 某学校准备购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买2个足球和3个篮球共需340元，购买5个足球和2个篮球共需410元．

(1)、购买一个足球、一个篮球各需多少元？

(2)、根据学校的实际情况，需购买足球和篮球共96个，并且总费用不超过5720元．问最多可以购买多少个篮球？

查看试题解析