陕西省宝鸡市陇县2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-01 类型：期末考试

进入出卷网下载

一、选择题（每小题只有一个选项是符合题意的，每小题3分，共30分）

1. 下列的式子一定是二次根式的是（）

A、 $\sqrt{-x - 2}$ B、 $\sqrt{x}$ C、 $\sqrt{x^{2} + 2}$ D、 $\sqrt{x^{2} - 2}$

查看试题解析
2. 以下列各组数为边长，不能构成直角三角形的是（）

A、3，4，5 B、1，1， $\sqrt{2}$ C、8，12，13 D、 $\sqrt{2}$ , $\sqrt{3}$ , $\sqrt{5}$

查看试题解析
3. 一次函数y=kx﹣1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（）

A、（﹣5，3） B、（1，﹣3） C、（5，﹣1） D、（2，2）

查看试题解析
4. 下列说法正确的是（）

A、矩形的对角线相等垂直 B、菱形的对角线相等 C、正方形的对角线相等 D、菱形的四个角都是直角

查看试题解析
5. 某校为了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们一周的读书时间进行了统计，统计数据如下表所示：

则该班学生一周读书时间的中位数和众数分别是（）

A、9， 8 B、9， 9 C、9.5， 9 D、9.5， 8

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 ${(3 \sqrt{2})}^{2} = 6$

查看试题解析
7. 如图，直线l是一次函数y=kx+b的图象，若点A（3，m）在直线l上，则m的值是（）

A、﹣5 B、 C、 D、7

查看试题解析
8. 如图，在平面直角坐标系中，四边形OABC为菱形，O（0，0），A（4，0），∠AOC=60°，则对角线交点E的坐标为（）

A、 $(2 ， \sqrt{3})$ B、 $(\sqrt{3} ， 2)$ C、 $(\sqrt{3} ， 3)$ D、 $(3 ， \sqrt{3})$

查看试题解析
9. 矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC=EF=2，CD=CE=1，则GH=（）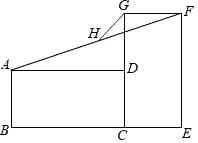

A、1 B、 $\frac{2}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
10. 甲、乙两车在某时间段内速度随时间变化的图象如图所示，下列结论：
①乙车前4秒行驶的总路程为48米；

②第3秒时，两车行驶的速度相同；

③甲在8秒内行驶了256米；

④乙车第8秒时的速度为2米/秒．

其中正确的是（）

A、①②③ B、①② C、①③④ D、①②④

查看试题解析

二、填空题（共4小题，每小题3分，计12分）

11. 若最简二次根式 $3 \sqrt{2 m + 5}$ 与 $5 \sqrt{4 m - 3}$ 可以合并，则m＝．

查看试题解析
12. 一组数据3，5，7，8，m的平均数为5，则这组数据的中位数是．

查看试题解析
13. 将直线y＝﹣x+8向下平移m个单位后，与直线y＝3x+6的交点在第二象限，则m的取值范围是．

查看试题解析
14.
如图，已知菱形ABCD的周长为16，面积为8 $\sqrt{3}$ ，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为．

查看试题解析

三、解答题（共8小题，计55分）

15. 计算：

(1)、 $2 \sqrt{12} \times \frac{\sqrt{3}}{4} \div \sqrt{2}$

(2)、 $\sqrt{3} \times (\sqrt{6} - \sqrt{2}) - (2 \sqrt{2} - 1)$

查看试题解析
16. 如图，已知直线l₁经过点A(－1，0)与点B(2，3)，另一条直线l₂经过点B，且与x轴交于点P(m，0)．

(1)、求直线l₁的解析式；

(2)、若△APB的面积为3，求m的值．

查看试题解析
17. 如图，在四边形ABCD中，AD∥BC，延长BC到E，使CE＝BC，连接AE交CD于点F，点F是CD的中点．求证：

(1)、△ADF≌△ECF．

(2)、四边形ABCD是平行四边形．

查看试题解析
18. 某射击队有甲、乙两名射手，他们各自射击7次，射中靶的环数记录如下：
甲：8，8，8，9，6，8，9

乙：10，7，8，8，5，10，8

(1)、分别求出甲、乙两名射手打靶环数的平均数、众数、中位数；

(2)、如果要选择一名成绩比较稳定的射手，代表射击队参加比赛，应如何选择？为什么？

查看试题解析
19. 已知：如图，在△ABC中，AB＝AC，AD是△ABC的中线，AN为△ABC的外角∠CAM的平分线，CE∥AD，交AN于点E．求证：四边形ADCE是矩形．

查看试题解析
20. 已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．

(1)、求证：四边形ABCD是菱形；

(2)、如果∠BDC=30°，DE=2，EC=3，求CD的长．

查看试题解析
21. 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．

(1)、求当x≥20时y与x的函数关系式；

(2)、若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方燃，使总费用最低，并求出最低费用．

查看试题解析
22. 如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中AF交EC于点M．
求证：△AHF为等腰直角三角形．

查看试题解析