海南省2020年中考数学试卷
试卷更新日期:2020-09-01 类型:中考真卷
一、选择题
-
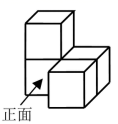
1. 实数3的相反数是( )A、 B、 C、3 D、2. 从海南省可再生能源协会2020年会上获悉,截至4月底,今年我省风电、光伏及生物质能的新能源发电量约 千瓦时.数据 可用科学记数法表示为( )A、 B、 C、 D、3. 如图是由 个相同的小正方体组成的几何体,则它的俯视图是( )
 A、
A、 B、
B、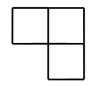 C、
C、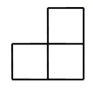 D、
D、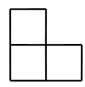 4. 不等式 的解集是( )A、 B、 C、 D、5. 在学校开展的环保主题实践活动中,某小组的 位同学捡拾废弃塑料袋的个数分别为: .这组数据的众数、中位数分别为( )A、 B、 C、 D、6. 如图,已知 直线 和 相交于点 若 ,则 等于( )
4. 不等式 的解集是( )A、 B、 C、 D、5. 在学校开展的环保主题实践活动中,某小组的 位同学捡拾废弃塑料袋的个数分别为: .这组数据的众数、中位数分别为( )A、 B、 C、 D、6. 如图,已知 直线 和 相交于点 若 ,则 等于( )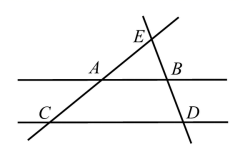 A、 B、 C、 D、7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( )
A、 B、 C、 D、7. 如图,在 中, 将 绕点 逆时针旋转得到 ,使点 落在 边上,连接 ,则 的长度是( ) A、 B、 C、 D、8. 分式方程 的解是( )A、 B、 C、 D、9. 下列各点中,在反比例函数 图象上的是( )A、(-1,8) B、(-2,4) C、(1,7) D、(2,4)10. 如图,已知 是 的直径, 是弦,若 则 等于( )
A、 B、 C、 D、8. 分式方程 的解是( )A、 B、 C、 D、9. 下列各点中,在反比例函数 图象上的是( )A、(-1,8) B、(-2,4) C、(1,7) D、(2,4)10. 如图,已知 是 的直径, 是弦,若 则 等于( ) A、 B、 C、 D、11. 如图,在 中, 的平分线交 于点 交 的延长线于点 于点 ,若 ,则 的周长为( )
A、 B、 C、 D、11. 如图,在 中, 的平分线交 于点 交 的延长线于点 于点 ,若 ,则 的周长为( ) A、 B、 C、 D、12. 如图,在矩形 中, 点 在 边上, 和 交于点 若 ,则图中阴影部分的面积为( )
A、 B、 C、 D、12. 如图,在矩形 中, 点 在 边上, 和 交于点 若 ,则图中阴影部分的面积为( )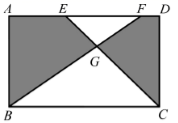 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解: = .14. 正六边形的每一个外角是度15. 如图,在 中, ,分别以点 为圆心,大于 的长为半径画弧,两弧相交于点 作直线 ,交 边于点 ,连接 ,则 的周长为.
 16. 海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.图是黎锦上的图案,每个图案都是由相同菱形构成的,若按照第 个图至第 个图中的规律编织图案,则第 个图中有个菱形, 第 个图中有个菱形(用含 的代数式表示).
16. 海南黎锦有着悠久的历史,已被列入世界非物质文化遗产名录.图是黎锦上的图案,每个图案都是由相同菱形构成的,若按照第 个图至第 个图中的规律编织图案,则第 个图中有个菱形, 第 个图中有个菱形(用含 的代数式表示).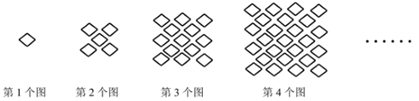
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 某村经济合作社决定把 吨竹笋加工后再上市销售,刚开始每天加工 吨,后来在乡村振兴工作队的指导下改进加工方法,每天加工 吨,前后共用 天完成全部加工任务,问该合作社改进加工方法前后各用了多少天?19. 新冠疫情防控期间,全国中小学开展“停课不停学”活动.某市为了解初中生每日线上学习时长 (单位:小时)的情况,在全市范围内随机抽取了 名初中生进行调查,并将所收集的数据分组整理,绘制了如图所示的不完整的频数分布直方图和扇形统计图.
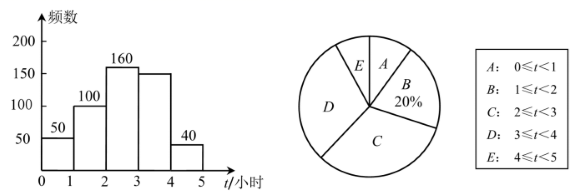
根据图中信息,解答下列问题:
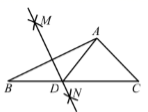
(1)、在这次调查活动中,采取的调查方式是(填写“全面调查”或“抽样调查”), .(2)、从该样本中随机抽取一名初中生每日线上学习时长,其恰好在“ ”范围的概率是;(3)、若该市有 名初中生,请你估计该市每日线上学习时长在“ ”范围的初中生有名.20. 为了促进海口主城区与江东新区联动发展,文明东越江通道将于今年底竣工通车.某校数学实践活动小组利用无人机测算该越江通道的隧道长度.如图, 隧道 在水平直线上,且无人机和隧道在同一个铅垂面内,无人机在距离隧道 米的高度上水平飞行,到达点 处测得点 的俯角为 继续飞行 米到达点 处,测得点 的俯角为 .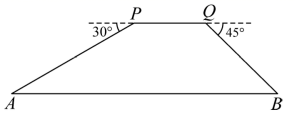 (1)、填空: 度, 度;(2)、求隧道 的长度(结果精确到 米).(参考数据: )21. 四边形 是边长为 的正方形, 是 的中点,连结 ,点 是射线 上一动点(不与点 重合),连结 ,交 于点 .(1)、如图1,当点 是 边的中点时,求证: ;
(1)、填空: 度, 度;(2)、求隧道 的长度(结果精确到 米).(参考数据: )21. 四边形 是边长为 的正方形, 是 的中点,连结 ,点 是射线 上一动点(不与点 重合),连结 ,交 于点 .(1)、如图1,当点 是 边的中点时,求证: ; (2)、如图2,当点 与点 重合时,求 的长;
(2)、如图2,当点 与点 重合时,求 的长;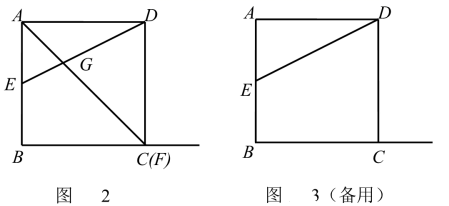 (3)、在点 运动的过程中,当线段 为何值时, ?请说明理由.22. 抛物线 经过点 和点 ,与 轴交于点 .(1)、求该抛物线的函数表达式;(2)、点 是该抛物线上的动点,且位于 轴的左侧.
(3)、在点 运动的过程中,当线段 为何值时, ?请说明理由.22. 抛物线 经过点 和点 ,与 轴交于点 .(1)、求该抛物线的函数表达式;(2)、点 是该抛物线上的动点,且位于 轴的左侧.①如图1,过点 作 轴于点 ,作 轴于点 ,当 时,求 的长;

②如图2,该抛物线上是否存在点 ,使得 ?若存在,请求出所有点 的坐标;若不存在,请说明理由.
