浙江省宁波市海曙区2020届九年级上学期数学开学试卷
试卷更新日期:2020-09-01 类型:开学考试
一、选择题
-
1. 若二次根式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、任何实数2. 下列标志中是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
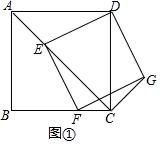
D、 3. 若关于 的一元二次方程 的一个根为 ,则 的值为( )A、 B、 或 C、 D、4. 下列条件中不能判定一定是平行四边形的有( )A、一组对角相等,一组邻角互补 B、一组对边平行,另一组对边相等 C、一组对边相等,一组对角相等 D、一组对边平行,且一条对角线平分另一条对角5. 用反证法证明“三角形中至少有一个内角不大于60°”,首先应假设这个三角形中( )A、没有一个角不小于60° B、没有一个角不大于60° C、所有内角不大于60° D、所有内角不小于60°6. “流浪地球“一上映就获得追捧,第一天票房约8亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达29.12亿元,若把增长率记作x,则方程可以记为( )A、8(1+x)=29.12 B、8 =29.12 C、8+8(1+x)+8 =29.12 D、8+8 =29.127. 一组数据1,2,3,3,4,5.若添加一个数据3,则下列统计量中,发生变化的是( )A、平均数 B、众数 C、中位数 D、方差8. 若菱形的两条对角线长是方程 的两个根,则该菱形的边长是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
3. 若关于 的一元二次方程 的一个根为 ,则 的值为( )A、 B、 或 C、 D、4. 下列条件中不能判定一定是平行四边形的有( )A、一组对角相等,一组邻角互补 B、一组对边平行,另一组对边相等 C、一组对边相等,一组对角相等 D、一组对边平行,且一条对角线平分另一条对角5. 用反证法证明“三角形中至少有一个内角不大于60°”,首先应假设这个三角形中( )A、没有一个角不小于60° B、没有一个角不大于60° C、所有内角不大于60° D、所有内角不小于60°6. “流浪地球“一上映就获得追捧,第一天票房约8亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达29.12亿元,若把增长率记作x,则方程可以记为( )A、8(1+x)=29.12 B、8 =29.12 C、8+8(1+x)+8 =29.12 D、8+8 =29.127. 一组数据1,2,3,3,4,5.若添加一个数据3,则下列统计量中,发生变化的是( )A、平均数 B、众数 C、中位数 D、方差8. 若菱形的两条对角线长是方程 的两个根,则该菱形的边长是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )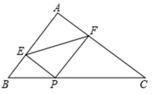 A、2 B、2.4 C、2.5 D、2.610. 如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、……、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、……、An-1An都在y轴上(n≥2),点P1(x1 , y1),点P2(x2 , y2),……,点Pn(xn , yn)在反比例函数y= (x>0)的图象上,已知B1(-1,1)则反比例函数解析式为( )
A、2 B、2.4 C、2.5 D、2.610. 如图,四边形OP1A1B1、A1P2A2B2、A2P3A3B3、……、An-1PnAnBn都是正方形,对角线OA1、A1A2、A2A3、……、An-1An都在y轴上(n≥2),点P1(x1 , y1),点P2(x2 , y2),……,点Pn(xn , yn)在反比例函数y= (x>0)的图象上,已知B1(-1,1)则反比例函数解析式为( ) A、y= B、y= C、y= D、y=
A、y= B、y= C、y= D、y=二、填空题
-
11. 已知 + =0,则 =.12. 某校规定学生的学期数学总评成绩由研究性学习成绩与期末卷面成绩共同决定,其中研究性学习成绩与期末卷面成绩所占比为2:3,小明的两项成绩依次是80分,90分,则小明这学期的数学成绩是.13. 已知一道斜坡的坡比为2: ,坡长39m,那么坡高为m.14. 已知关于x的方程x2-2 x-k=0有两个相等的实数根,则k的值为.15. 如图,在四边形ABCD中, ∠ADC +∠BCD =220°, E、F分别是AC、BD的中点,P是AB边上的中点,则∠EPF= .
 16. 如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD= .
16. 如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD= .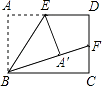 17. 如图,过原点的直线与反比例函数y= (x>0)、反比例函数y= (x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y= (x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为 .
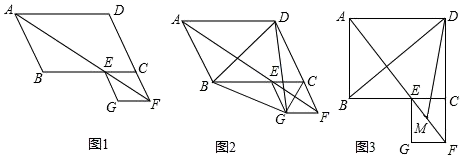
17. 如图,过原点的直线与反比例函数y= (x>0)、反比例函数y= (x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y= (x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为 .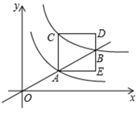 18. 如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为.
18. 如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为.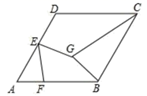
三、解答题
-
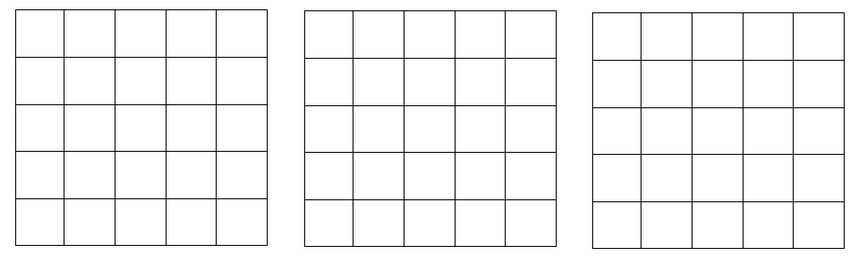
19.(1)、计算: -4 +(2)、解方程:(x-2)²=2(x-2)20. 如图每个小方格都是边长为1的正方形,在图中添加阴影,使阴影部分既是轴对称图形,又是中心对称图形,且阴影部分的面积是9,请在三个图形各画出一幅图形,所画的三幅图形互不全等.
 21. 如图,已知一次函数y=x﹣2与反比例函数y= 的图象交于A、B两点.
21. 如图,已知一次函数y=x﹣2与反比例函数y= 的图象交于A、B两点. (1)、求A、B两点的坐标;(2)、观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;(3)、坐标原点为O,求△AOB的面积.22. 在宁波慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图。
(1)、求A、B两点的坐标;(2)、观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;(3)、坐标原点为O,求△AOB的面积.22. 在宁波慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图。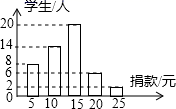 (1)、这50名同学捐款的众数为元,中位数为元;(2)、该校共有600名学生参与捐款,请估计该校学生的捐款总数。23. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.(1)、若将这种水果每斤的售价降低x元,则每天的销售量是 斤。(用含x的代数式表示)(2)、销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
(1)、这50名同学捐款的众数为元,中位数为元;(2)、该校共有600名学生参与捐款,请估计该校学生的捐款总数。23. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.(1)、若将这种水果每斤的售价降低x元,则每天的销售量是 斤。(用含x的代数式表示)(2)、销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?