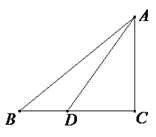初中数学青岛版九年级上学期 第2章 2.4 解直角三角形
试卷更新日期:2020-08-29 类型:同步测试
一、单选题
-
1. 已知在Rt△ABC中,∠C=90°,AB=5,AC=3,则tanA的值( )A、 B、 C、 D、2. 如图,在△ABC中,CA=CB=4,cosC= ,则sinB的值为( )
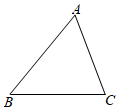 A、 B、 C、 D、3. 如图,梯子AC的长为2.8米,则梯子顶端离地面的高度AD是( )
A、 B、 C、 D、3. 如图,梯子AC的长为2.8米,则梯子顶端离地面的高度AD是( )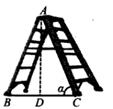 A、 米 B、 米 C、 sinα米 D、 cosα米4. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°= = = =2﹣ .类比这种方法,计算tan22.5°的值为( )
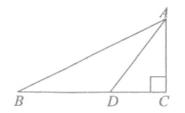
A、 米 B、 米 C、 sinα米 D、 cosα米4. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°= = = =2﹣ .类比这种方法,计算tan22.5°的值为( )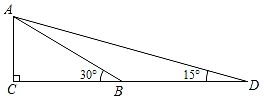 A、 +1 B、 ﹣1 C、 D、5. 如图,△ACB中,∠ACB=90°,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )
A、 +1 B、 ﹣1 C、 D、5. 如图,△ACB中,∠ACB=90°,已知∠B=α,∠ADC=β,AB=a,则BD的长可表示为( )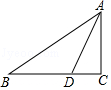 A、a•(cosα﹣cosβ) B、 C、acosα﹣ D、a•cosα﹣asinα•a•tanβ6. 如图所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知大桥主架顶端离水面的高CD=a , 则此时测量点与大桥主架的水平距离AB为( )
A、a•(cosα﹣cosβ) B、 C、acosα﹣ D、a•cosα﹣asinα•a•tanβ6. 如图所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知大桥主架顶端离水面的高CD=a , 则此时测量点与大桥主架的水平距离AB为( )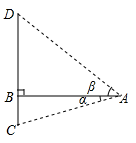 A、asinα+asinβ B、atanα+atanβ C、 D、7. 如图, 中, , , ,则 的长为( )
A、asinα+asinβ B、atanα+atanβ C、 D、7. 如图, 中, , , ,则 的长为( ) A、 B、 C、5 D、8. 如图,为了保证道路交通安全,某段高速公路在A处设立观测点,与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒。若∠BAC=α,则此车的速度为( )
A、 B、 C、5 D、8. 如图,为了保证道路交通安全,某段高速公路在A处设立观测点,与高速公路的距离AC为20米.现测得一辆小轿车从B处行驶到C处所用的时间为4秒。若∠BAC=α,则此车的速度为( )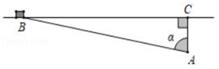 A、5tanα米/秒 B、80tanα米/秒 C、 米/秒 D、 米/秒9. 如图所示的网格是正方形网格,点A,B,C都在格点上,则tan∠BAC的值为( )
A、5tanα米/秒 B、80tanα米/秒 C、 米/秒 D、 米/秒9. 如图所示的网格是正方形网格,点A,B,C都在格点上,则tan∠BAC的值为( ) A、2 B、 C、 D、10. 如图,BD是菱形ABCD的对角线,CE⊥AB于点E,且点E是AB的中点,则tan∠BFE的值是( )
A、2 B、 C、 D、10. 如图,BD是菱形ABCD的对角线,CE⊥AB于点E,且点E是AB的中点,则tan∠BFE的值是( )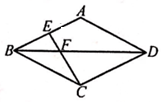 A、 B、 C、2 D、11. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是( )
A、 B、 C、2 D、11. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是( )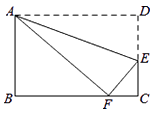 A、 B、 C、 D、12. 如图,在菱形ABCD中,DE⊥AB, ,AE=3,则tan∠DBE的值是( )
A、 B、 C、 D、12. 如图,在菱形ABCD中,DE⊥AB, ,AE=3,则tan∠DBE的值是( )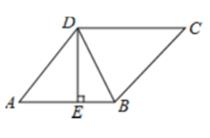 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
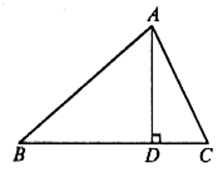
13. 在 中, , 为BC边上的高, ,则BC的长为 .14. 如图,将一副三角板按图中方式叠放,BC=4,那么BD=
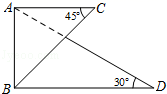 15. 在△ABC中,AC=5,AB=6,则△ABC面积的最大值为.16. 如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8,现将△ABC折叠,使点A与点B重合,折痕为DE,则tan∠CBE=.
15. 在△ABC中,AC=5,AB=6,则△ABC面积的最大值为.16. 如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8,现将△ABC折叠,使点A与点B重合,折痕为DE,则tan∠CBE=.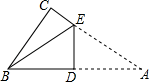 17. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE= m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。
17. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE= m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。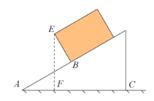 18. 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM= ,则tan∠B= .
18. 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM= ,则tan∠B= .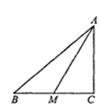 19. 如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是.
19. 如图,∠MAN=60°,若△ABC的顶点B在射线AM上,且AB=2,点C在射线AN上运动,当△ABC是锐角三角形时,BC的取值范围是. 20. 如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为(结果保留根号)
20. 如图1,含30°和45°角的两块三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm,点P为边BC(EF)的中点,现将三角板ABC绕点P按逆时针方向旋转角度α(如图2),设边AB与EF相交于点Q,则当a从0°到90°的变化过程中,点Q移动的路径长为(结果保留根号)
三、解答题
-
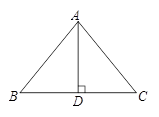
21. 我们把底角为51°的等腰三角形称为最稳定三角形. 如图,已知△ABC是最稳定三角形, AB=AC,BC=232.8m.求BC边上的高AD的长.
(sin51°≈0.8,cos51°≈0.6,tan51°≈1.2,精确到1m)
 22. 如图,在 中, 的平分线 交 于点 .求 的长?
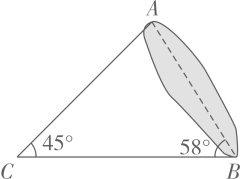
22. 如图,在 中, 的平分线 交 于点 .求 的长?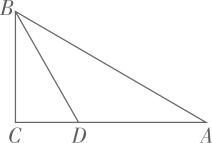 23. 如图示,在 中, , , ,求 的面积.
23. 如图示,在 中, , , ,求 的面积. 24. 在△ABC中,tanA= ,tanB=1,CD⊥AB于点D,且BD=4,请画出示意图并且求边AB的长.25. 如图,在Rt△ABC中,∠C=90,BC=8,tanB= ,点D在BC上,且BD=AD。求AC的长和cos∠ADC的值。
24. 在△ABC中,tanA= ,tanB=1,CD⊥AB于点D,且BD=4,请画出示意图并且求边AB的长.25. 如图,在Rt△ABC中,∠C=90,BC=8,tanB= ,点D在BC上,且BD=AD。求AC的长和cos∠ADC的值。