江西省抚州市安县五校2019-2020学年八年级上学期数学10月月考试卷
试卷更新日期:2020-08-28 类型:月考试卷
一、单选题
-
1. 数字 , , , ,2.010010001, 中无理数的个数有( )A、1个 B、2个 C、3个 D、4个2. 下列说法错误的是( )A、 的相反数是-7 B、-1的立方根是-1 C、 是2的算术平方根 D、-3是-9的平方根3. 在下列四组数中,不是勾股数的一组数是( )A、a=15,b=8,c=17 B、a=9,b=12,c=15 C、a=7,b=24,c=25 D、a=3,b=5,c=74. 设面积为7的正方形的边长为x,那么关于x的说法正确的是( )A、x是有理数 B、 C、x不存在 D、x是2和3之间的实数5. 三国时期吴国赵爽创造了“勾股圆方图”(如图)证明了勾股定理,在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的一个小正方形EFGH组成的,已知小正方形的边长是2,每个直角三角形的短直角边长是6,则大正方形ABCD的面积是( )
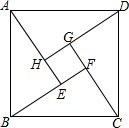 A、36 B、40 C、64 D、1006. 若一个直角三角形的两直角边的长为12和5,则第三边的长为( )A、13或 B、13或15 C、13 D、15
A、36 B、40 C、64 D、1006. 若一个直角三角形的两直角边的长为12和5,则第三边的长为( )A、13或 B、13或15 C、13 D、15二、填空题
-
7. 已知 ,则 .8. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC= .
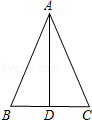 9. 如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为8cm,则正方形A、B、C、D的面积和是cm2.
9. 如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为8cm,则正方形A、B、C、D的面积和是cm2.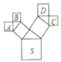 10. 如图,在高3米,坡面线段距离AB为5米的楼梯表面铺地毯,则地毯长度至少需米.
10. 如图,在高3米,坡面线段距离AB为5米的楼梯表面铺地毯,则地毯长度至少需米. 11. 如图,有一个数值转换器,流程如下,当输入的x为256时,输出的y是.
11. 如图,有一个数值转换器,流程如下,当输入的x为256时,输出的y是.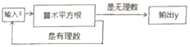 12. 已知 , ,则 的值为.
12. 已知 , ,则 的值为.三、解答题
-
13.(1)、计算: ;
(2)、已知 2m-1 的平方根是±3,5n+32的立方根是-2,求m,n的值.
14. 求下列各式中的x(1)、(2)、15. 如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图: (1)、在图①中画一条线段MN , 使MN= ;(2)、在图②中画一个三边长均为无理数,且各边都不相等的直角△DEF .16. 已知△ABC的三边 , , .(1)、求证:△ABC是直角三角形;(2)、利用第(1)题的结论,写出两组m,n的值,要求三角形边长均为整数.17. 用一张面积为900cm2的正方形纸片,能否裁出一块面积为600cm2 , 长与宽的比为5:3的长方形纸片吗?为什么?18. 定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)、在图①中画一条线段MN , 使MN= ;(2)、在图②中画一个三边长均为无理数,且各边都不相等的直角△DEF .16. 已知△ABC的三边 , , .(1)、求证:△ABC是直角三角形;(2)、利用第(1)题的结论,写出两组m,n的值,要求三角形边长均为整数.17. 用一张面积为900cm2的正方形纸片,能否裁出一块面积为600cm2 , 长与宽的比为5:3的长方形纸片吗?为什么?18. 定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点. (1)、已知M、N把线段分割成AM、MN、NB,若 , , ,则点M、N是线段AB的勾股分割点吗?请说明理由.(2)、已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.19. 如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)、已知M、N把线段分割成AM、MN、NB,若 , , ,则点M、N是线段AB的勾股分割点吗?请说明理由.(2)、已知M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.19. 如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20. (1)、求CD的长;(2)、求AB的长;(3)、判断△ABC的形状.20. 如图,已知正方体纸盒的表面积为12cm2;
(1)、求CD的长;(2)、求AB的长;(3)、判断△ABC的形状.20. 如图,已知正方体纸盒的表面积为12cm2;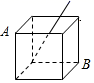 (1)、求正方体的棱长;(2)、剪去盖子后,插入一根长为5cm的细木棒,则细木棒露在外面的最短长度是多少?(3)、一只蚂蚁在纸盒的表面由A爬到B,求蚂蚁行走的最短路线.21. 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.
(1)、求正方体的棱长;(2)、剪去盖子后,插入一根长为5cm的细木棒,则细木棒露在外面的最短长度是多少?(3)、一只蚂蚁在纸盒的表面由A爬到B,求蚂蚁行走的最短路线.21. 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.
 (1)、当t=2时,CD= , AD= ;(2)、求当t为何值时,△CBD是直角三角形,说明理由;(3)、求当t为何值时,△CBD是以BD或CD为底的等腰三角形?并说明理由.22. 阅读下面的文字,解答问题:
(1)、当t=2时,CD= , AD= ;(2)、求当t为何值时,△CBD是直角三角形,说明理由;(3)、求当t为何值时,△CBD是以BD或CD为底的等腰三角形?并说明理由.22. 阅读下面的文字,解答问题:大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用 -1来表示 的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵ ,即 ,
∴ 的整数部分为2,小数部分为( -2).
请解答:
(1)、 的整数部分是 , 小数部分是.(2)、如果 的小数部分为a , 的整数部分为b , 求a+b- 的值;(3)、已知: 10+ =x+y , 其中x是整数,且0<y<1,求x-y的相反数.23. 如图1,在 的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点D、A同时出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点C时,两个点都停止运动. (1)、请在 的网格纸图2中画出运动时间t为2秒时的线段PQ并求其长度;(2)、在动点P、Q运动的过程中,△PQB能否成为PQ=BQ的等腰三角形?若能,请求出相应的运动时间t;若不能,请说明理由;(3)、在(1)中的图2中,点E如图所示,是否在PQ上存在一点M,使DM+EM的值最小,如存在,求出DM+EM最小值;如不存在,说明理由.
(1)、请在 的网格纸图2中画出运动时间t为2秒时的线段PQ并求其长度;(2)、在动点P、Q运动的过程中,△PQB能否成为PQ=BQ的等腰三角形?若能,请求出相应的运动时间t;若不能,请说明理由;(3)、在(1)中的图2中,点E如图所示,是否在PQ上存在一点M,使DM+EM的值最小,如存在,求出DM+EM最小值;如不存在,说明理由.