青岛版数学九年级上册第一章《图形的相似》单元测试
试卷更新日期:2020-08-28 类型:单元试卷
一、单选题
-
1.
在如图所示的四个图形为两个圆或相似的正多边形,其中位似图形的个数为( )
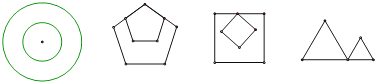 A、1个 B、2个 C、3个 D、4个2. 关于对位似图形的4个表述中:
A、1个 B、2个 C、3个 D、4个2. 关于对位似图形的4个表述中:①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
正确的个数( )
A、1个 B、2个 C、3个 D、4个3. 如图,已知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( )①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
 A、1 B、2 C、3 D、44. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A、1 B、2 C、3 D、44. 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )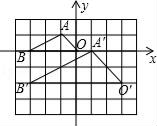 A、(0,0) B、(0,1) C、(﹣3,2) D、(3,﹣2)5. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的 ,那么点B'的坐标是( )
A、(0,0) B、(0,1) C、(﹣3,2) D、(3,﹣2)5. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的 ,那么点B'的坐标是( )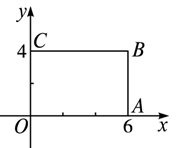 A、(3,2) B、(-2,-3) C、(2,3)或(-2,-3) D、(3,2)或(-3,-2)6. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△DOE与S△COE的比是( )
A、(3,2) B、(-2,-3) C、(2,3)或(-2,-3) D、(3,2)或(-3,-2)6. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△DOE与S△COE的比是( ) A、1:25 B、1:5 C、1:4 D、1:37. 如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长交AC于点F,则AF:FC的值是( )
A、1:25 B、1:5 C、1:4 D、1:37. 如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长交AC于点F,则AF:FC的值是( ) A、3:2 B、4:3 C、2:1 D、2:38. 路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( )
A、3:2 B、4:3 C、2:1 D、2:38. 路边有一根电线杆AB和一块长方形广告牌,有一天小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在长方形广告牌的上边中点G处,而长方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,长方形广告牌的长HF=4米,高HC=3米,DE=4米,则电线杆AB的高度是( ) A、6.75米 B、7.75米 C、8.25米 D、10.75米9. 如图, , , , , , , ,则 的度数为( )
A、6.75米 B、7.75米 C、8.25米 D、10.75米9. 如图, , , , , , , ,则 的度数为( )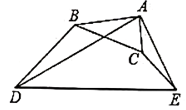 A、 B、 C、 D、无法确定10. 如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC与点G,则下列结论中错误的是( )
A、 B、 C、 D、无法确定10. 如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC与点G,则下列结论中错误的是( ) A、△CGE∽△CBP B、△APD∽△PGD C、△APG∽△BFP D、△PCF∽△BCP11. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A、△CGE∽△CBP B、△APD∽△PGD C、△APG∽△BFP D、△PCF∽△BCP11. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )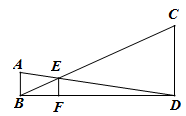 A、 B、 C、 D、12. 如图在正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A、 B、 C、 D、12. 如图在正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( ) A、
A、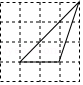 B、
B、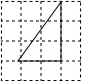 C、
C、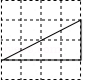 D、
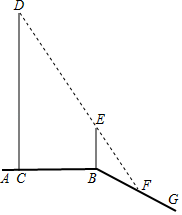
D、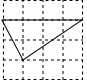
二、填空题
-
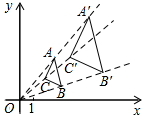
13. 四边形ABCD与四边形A'B'C'D'位似,点O为位似中心.若AB:A'B'=2:3,则OB:OB'=.14. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为.
 15. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为米(精确到0.1米).
15. 为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索:根据《科学》中光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.4米,观察者目高CD=1.6米,则树(AB)的高度约为米(精确到0.1米).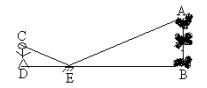 16. 如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为 ,点E的坐标为 ,则点P的坐标为 .
16. 如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为 ,点E的坐标为 ,则点P的坐标为 . 17. 如图所示,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值为.
17. 如图所示,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,求PE+PF的值为.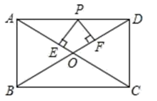 18. 如图,正方形ABCD中, E是AD的中点,点F在CD上,且CF=3FD,若 ,则EF的长等于.
18. 如图,正方形ABCD中, E是AD的中点,点F在CD上,且CF=3FD,若 ,则EF的长等于. 19. 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为 .
19. 如图,直线y=x+1与x轴交于点A,与y轴交于点B,△BOC与△B′O′C′是以点A为位似中心的位似图形,且相似比为1:3,则点B的对应点B′的坐标为 .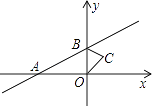 20. 在平行四边形ABCD中,E为CD的中点,△DOE的面积是2,△DOA的面积 .
20. 在平行四边形ABCD中,E为CD的中点,△DOE的面积是2,△DOA的面积 .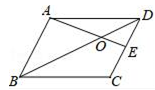
三、解答题
-
21. 在矩形ABCD中,F是BC上一点,AF的延长线交DC的延长线于G,DE⊥AG于E.根据上述条件,请在图中找出四组相似三角形,并说明其中一组的理由.
 22. 如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AD于点E,交BC的延长线于点F.求证:△ABF∽△CAF.
22. 如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AD于点E,交BC的延长线于点F.求证:△ABF∽△CAF. 23. 如图,△ABC中,AB=10cm,BC=20cm,点P从A开始沿AB边向B点以1cm/s的速度移动,到达点B时停止.点Q从点B开始沿BC边向C点以2cm/s的速度移动,到达点C时停止.如果P、Q分别从A、B同时出发,经几秒种△PBQ与△ABC相似?
23. 如图,△ABC中,AB=10cm,BC=20cm,点P从A开始沿AB边向B点以1cm/s的速度移动,到达点B时停止.点Q从点B开始沿BC边向C点以2cm/s的速度移动,到达点C时停止.如果P、Q分别从A、B同时出发,经几秒种△PBQ与△ABC相似?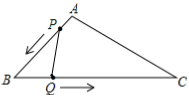 24. 如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面1.5m,竹标顶端离地面2.4m,小明到竹杆的距离DF=2m,竹杆到塔底的距离DB=32m,求这座古塔的高度.
24. 如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面1.5m,竹标顶端离地面2.4m,小明到竹杆的距离DF=2m,竹杆到塔底的距离DB=32m,求这座古塔的高度.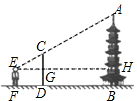 25. 如图,小超想要测量窗外的路灯 的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点 落在地板 处、窗户的最低点落在地板是 处,小超测得窗户距地面的高度 ,窗高 ,并测得 , .请根据以上测量数据,求窗外的路灯 的高度.
25. 如图,小超想要测量窗外的路灯 的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点 落在地板 处、窗户的最低点落在地板是 处,小超测得窗户距地面的高度 ,窗高 ,并测得 , .请根据以上测量数据,求窗外的路灯 的高度.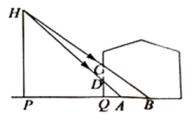 26. 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
26. 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.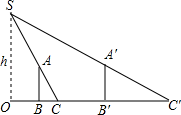 27. 如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
27. 如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.