初中数学苏科版九年级上册2.3 确定圆的条件 同步测试
试卷更新日期:2020-08-28 类型:同步测试
一、单选题
-
1. 现有如下4个命题:
①过两点可以作无数个圆.②三点可以确定一个圆.③任意一个三角形有且只有一个外接圆.④任意一个圆有且只有一个内接三角形.其中正确的有
A、1个 B、2个 C、3个 D、4个2. 若三角形的外心在这个三角形的一边上,则这个三角形是( ).A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
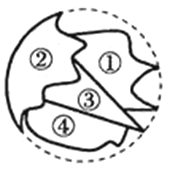 A、第①块; B、第②块; C、第③块; D、第④块.4. 一个点到圆的最大距离为9 cm,最小距离为3 cm,则圆的半径为( )A、3 cm或6 cm B、6 cm C、12 cm D、12 cm或6 cm5. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
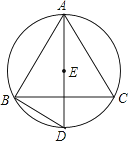
A、第①块; B、第②块; C、第③块; D、第④块.4. 一个点到圆的最大距离为9 cm,最小距离为3 cm,则圆的半径为( )A、3 cm或6 cm B、6 cm C、12 cm D、12 cm或6 cm5. 如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )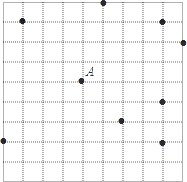 A、2 <r< B、 <r≤3 C、 <r<5 D、5<r<6. Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则它的外心与直角顶点的距离是为( )A、2cm B、2.5cm C、3cm D、4cm7. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点△ABC的外部,则下列叙述正确的是( ).
A、2 <r< B、 <r≤3 C、 <r<5 D、5<r<6. Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则它的外心与直角顶点的距离是为( )A、2cm B、2.5cm C、3cm D、4cm7. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点△ABC的外部,则下列叙述正确的是( ).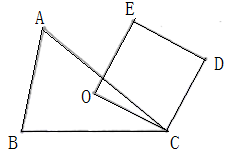 A、D是△AEB的外心,O是△AED的外心 B、O不是△AEB的外心,O不是△AED的外心 C、D不是△AEB的外心,O是△AED的外心 D、O是△AEB的外心,O不是△AED的外心8. 如图,在△ABC中,∠ACB=90°,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切于点M , P、Q分别是边BC和半圆上的动点,连接PQ , 则PQ长的最小值是( )
A、D是△AEB的外心,O是△AED的外心 B、O不是△AEB的外心,O不是△AED的外心 C、D不是△AEB的外心,O是△AED的外心 D、O是△AEB的外心,O不是△AED的外心8. 如图,在△ABC中,∠ACB=90°,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切于点M , P、Q分别是边BC和半圆上的动点,连接PQ , 则PQ长的最小值是( )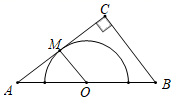 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 锐角三角形的外心在 , 直角三角形的外心在 ,钝角三角形的外心在.10. 直角三角形的两条直角边分别为5cm和12cm , 则其外接圆半径长为 .11. 在Rt△ABC中 ,∠C=90°,AC=2 , BC=4,若以点C为圆心,AC为半径作圆,则AB边的中点E与⊙C的位置关系为 .
12. 在平面直角坐标系中有 , , 三点, , , .现在要画一个圆同时经过这三点,则圆心坐标为 .13. 已知△ABC的三边a,b,c,满足a+b2+|c﹣6|+28=4 +10b,则△ABC的外接圆半径= .14. 如图,在4×4的网格图中,A、B、C是三个格点,其中每个小正方形的边长为1,△ABC的外心可能是M、N、P、Q四个点中的一个点 . 15. 在平面直角坐标系中,点A、B、C的坐标分别为 、 、 ,点E是 的外接圆上一点,BE交线段AC于点D,若 ,则点D的坐标为.
15. 在平面直角坐标系中,点A、B、C的坐标分别为 、 、 ,点E是 的外接圆上一点,BE交线段AC于点D,若 ,则点D的坐标为. 16. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .
16. 如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为 .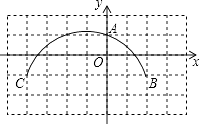
三、解答题
-
17. 如图,已知等腰△ABC,AB=AC=8,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.