初中数学苏科版九年级上册 2.2 圆的对称性 同步测试
试卷更新日期:2020-08-28 类型:同步测试
一、单选题
-
1. 下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有( )A、1个 B、2个 C、3个 D、4个2. 如图,在⊙O中, = ,∠A=40°,则∠B的度数是( )
 A、60° B、40° C、50° D、70°3. 将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这个扇形圆心角的度数为( )A、30°,60°,90° B、60°,120°,180° C、50°,100°,150° D、80°,120°,160°4. 如图,已知点A,B,C,D,E是⊙O的五等分点,则∠BAD的度数是( )
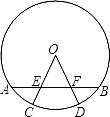
A、60° B、40° C、50° D、70°3. 将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,则这个扇形圆心角的度数为( )A、30°,60°,90° B、60°,120°,180° C、50°,100°,150° D、80°,120°,160°4. 如图,已知点A,B,C,D,E是⊙O的五等分点,则∠BAD的度数是( )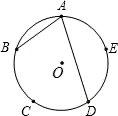 A、36° B、48° C、72° D、96°5. 如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB的长为( )
A、36° B、48° C、72° D、96°5. 如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB的长为( ) A、8 B、12 C、16 D、26. 已知⊙O的半径是10cm, 是120°,那么弦AB的弦心距是( )
A、8 B、12 C、16 D、26. 已知⊙O的半径是10cm, 是120°,那么弦AB的弦心距是( ) A、5cm B、 cm C、 cm D、 cm7. 如图,在⊙O中 = ,∠AOB=40°,则∠COD的度数( )
A、5cm B、 cm C、 cm D、 cm7. 如图,在⊙O中 = ,∠AOB=40°,则∠COD的度数( ) A、20° B、40° C、50° D、60°8. 为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
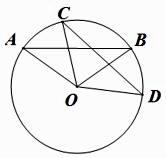
A、20° B、40° C、50° D、60°8. 为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( ) A、12cm B、10cm C、8cm D、6cm9. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( )
A、12cm B、10cm C、8cm D、6cm9. 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( ) A、AB=AD B、BC=CD C、 D、∠BCA=∠DCA10. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm
A、AB=AD B、BC=CD C、 D、∠BCA=∠DCA10. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm二、填空题
-
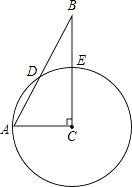
11. 过圆内的一点(非圆心)有条弦,有条直径.12. 已知弦AB把圆周分成1:5的两部分,则弦AB所对的圆心角的度数为度。13. 在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为 .14. 如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC与点E.则 的度数为 .
 15. 如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是.
15. 如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是. 16. 如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是.17.
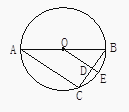
16. 如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是.17.如图,AB为⊙O直径,E是BC中点,OE交BC于点D,BD=3,AB=10,则AC= .
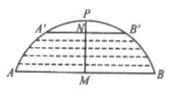
 18. 如图,MN是⊙O的直径,MN=8,∠AMN=20°,点B为弧 的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 .
18. 如图,MN是⊙O的直径,MN=8,∠AMN=20°,点B为弧 的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 .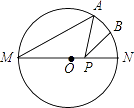
三、解答题