初中数学北师大版八年级上学期 第一章测试卷
试卷更新日期：2020-08-27 类型：单元试卷
一、单选题
-
1. 下列选项中，是直角三角形的三边长的是（ ）A、 1，2，3 B、 2，3，4 C、 3，4，5 D、 4，5，62. 如果将直角三角形的两直角边同时扩大到原来的2倍，那么斜边扩大到原来的（ ）A、2倍 B、4倍 C、3倍 D、以上结论都不对3. 下列各组数为边长，能构成直角三角形的是（ ）A、2、3、4 B、3、4、6 C、5、12、13 D、6、7、114. 如图，正方体的棱长为4cm，A是正方体的一个顶点，B是侧面正方形对角线的交点．一只蚂蚁在正方体的表面上爬行，从点A爬到点B的最短路径是（ ）
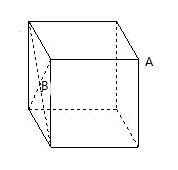A、9 B、 C、 D、125. 如图，一客轮以16海里/时的速度从港口A出发向东北方向航行，另一客轮同时以12海里/时的速度从港口A出发向东南方向航行，离开港口2小时后，则两船相距（ ）
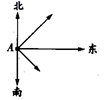A、25海里 B、30海里 C、35海里 D、40海里6. 若 Rt ABC 中，∠C＝90°，且 AB＝10，BC＝8，则 AC 的值是（ ）A、5 B、6 C、7 D、87. 将一根 24cm 的筷子，置于底面直径为 15cm ， 高 8cm 的装满水的无盖圆柱形水杯中，设筷子浸没在杯子里面的长度为 hcm ， 则 h 的取值范围是（ ）A、h≤15cm B、h≥8cm C、8cm≤h≤17cm D、7cm≤h≤16cm8. 《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线长恰好相等．问门高、宽和对角线的长各是多少？设门对角线的长为x尺，下列方程正确的是（ ）A、（x+2）2+（x﹣4）2＝x2 B、（x﹣2）2+（x﹣4）2＝x2 C、x2+（x﹣2）2＝（x﹣4）2 D、（x﹣2）2+x2＝（x+4）2二、填空题
-
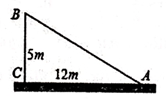
9. 如图，一根垂直于地面的旗杆在离地面5m处撕裂折断，旗杆顶部落在离旗杆底部12m处，旗杆折断之前的高度是。
10. 图中阴影部分是一个正方形，则此正方形的面积为 ．
11. 如图是一株美丽的勾股树，其作法为：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作两个正方形，计为②．依此类推…若正方形①的面积为16，则正方形③的面积是 ．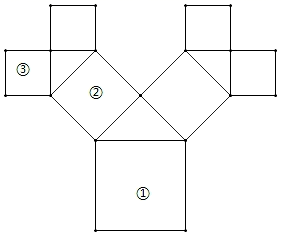
12. 活动楼梯如图所示，∠B＝90°，斜坡AC的坡度为1：1，斜坡AC的坡面长度为8m，则走这个活动楼梯从A点到C点上升的高度BC为 ．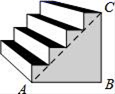
三、解答题
-
13. 如图，小颖和她的同学荡秋千，秋千AB在静止位置时，下端B离地面0.6m，荡秋千到AB的位置时，下端B距静止位置的水平距离EB等于2.4m，距地面1.4m，求秋千AB的长.
14. 为整治城市街道的汽车超速现象，交警大队在某街道旁进行了流动测速.如图，一辆小汽车在某城市街道上直行，某一时刻刚好行驶到离车速检测仪 的 处，过了 后，小汽车到达离车速检测仪 的 处，已知该段城市街道的限速为 ，请问这辆小汽车是否超速？
四、综合题
-
15. 如图，正方形网格中的两个小正方形的边长都是 ，每个小正方形的顶点叫格点，一个顶点为格点的三角形称为格点三角形：
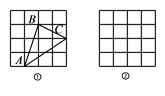(1)、如图①，已知格点 ，则 （是或不是）直角三角形：(2)、画一个格点 ，使其为钝角三角形，且面积为16. 如图，在Rt△ABC中，∠ACB=90°，D为边AC上一点，且BC=3CD，BD=10。
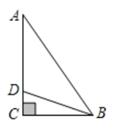(1)、求CD的长；(2)、若AB=5 ，求AD的长。17. 定义：若一个三角形两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，这两边的交点称为勾股顶点。
(1)、如图①，已知△ABC为勾股高三角形，其中A为勾股顶点，AD是BC边上的高。若BD=3，CD=4，求高AD的长；(2)、如图②，在钝角三角形ABC中，∠BAC为钝角，CH是AB边上的高，若BH=AC，求证：△ABC是勾股高三角形；(3)、如图③，△ABC中，AB=AC=2(其中BC<2)，若△ABC为勾股高三角形，求cosA的值。18. 如图，居民楼与马路是平行的，在一楼的点A处测得它到马路的距离为9m，已知在距离载重汽车41m处就可受到噪声影响.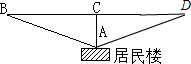
(1)、试求在马路上以4m/s速度行驶的载重汽车，能给一楼A处的居民带来多长时间的噪音影响？(2)、若时间超过25秒，则此路禁止该车通行，你认为载重汽车可以在这条路上通行吗？