高中数学人教新课标A版 选修2-1 3.1空间向量及其运算
试卷更新日期:2020-08-27 类型:同步测试
一、单选题
-
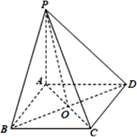
1. 已知空间向量 , ,若 ,则实数 ( )A、-2 B、-1 C、1 D、22. 已知 , ,若 ,则( )A、 B、 C、 D、3. 已知向量 ,则下列向量中与 成 的是( )A、 B、 C、 D、4. 已知点 与点 ,则 之间的距离为( )A、 B、 C、 D、5. 已知向量 , ,则 等于( )A、1 B、 C、3 D、96. 已知平面向量 , 满足 , ,则 在 方向上的投影为( )A、1 B、2 C、3 D、47. 已知三棱柱 的侧棱与底面边长都相等, 在底面ABC内的射影为 的中心O,则 与底面ABC所成角的余弦值等于( )A、 B、 C、 D、8. 若向量 ,且 与 的夹角余弦为 ,则 等于( )A、 B、 C、 或 D、29. 如图,在三棱锥 中, , , 两两垂直,且 , 为 中点,则 等于( )
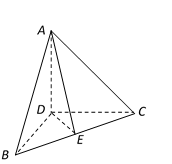 A、3 B、2 C、1 D、010. 设平面α的法向量为(1,2,﹣2),平面β的法向量为(﹣2,﹣4,k),若α∥β,则k=( )A、2 B、﹣4 C、4 D、﹣211. 已知 为直线l的方向向量, , 分别为平面 , 的法向量 不重合 那么下列说法中:
A、3 B、2 C、1 D、010. 设平面α的法向量为(1,2,﹣2),平面β的法向量为(﹣2,﹣4,k),若α∥β,则k=( )A、2 B、﹣4 C、4 D、﹣211. 已知 为直线l的方向向量, , 分别为平面 , 的法向量 不重合 那么下列说法中:; ; ; 正确的有
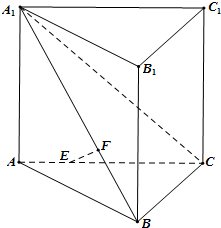
A、1个 B、2个 C、3个 D、4个12. 如图所示,在长方体ABCDA1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB的中点,则点E到平面ACD1的距离为( )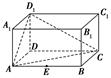 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
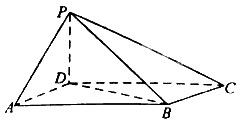
13. 已知直线l与平面 垂直,直线 的一个方向向量为 ,向量 与平面 平行,则 .14. 已知 , ,且 ,则 .15. 圆O为△ABC的外接圆,半径为2,若 ,且 ,则向量 在向量 方向上的投影为.16. 四棱锥 中, 平面 ,底面 是正方形,且 ,则直线 与平面 所成角为 .
三、解答题
-
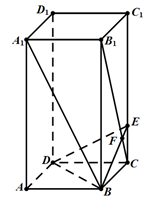
17. 已知向量 =(1,-3,2), =(-2,1,1),点A(-3,-1,4),B(-2,-2,2).(1)、求|2 + |;(2)、在直线AB上,是否存在一点E,使得 ⊥ ?(O为原点)18. 已知空间三点 ,设 .(1)、求 和 的夹角 的余弦值;(2)、若向量 与 互相垂直,求 的值.19. 在三棱柱 中,已知 , , 为 的中点, 平面
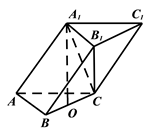 (1)、证明四边形 为矩形;(2)、求直线 与平面 所成角的余弦值.
(1)、证明四边形 为矩形;(2)、求直线 与平面 所成角的余弦值.