初中数学北师大版八年级上学期 第一章 1.1探索勾股定理
试卷更新日期：2020-08-27 类型：同步测试
一、单选题
-
1. 如图，以Rt△ABC的三边为直角边分别向外作等腰直角三角形．若AB= ，则图中阴影部分的面积为（ ）
A、 B、 C、 D、52. 如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，则AB的长为（ ）
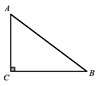A、5 B、25 C、6 D、3. 如图，以Rt△ABC的三边为边，分别向外作正方形，它们的面积分别为S1、S2、S3 ， 若S1+S2+S3=16，则S1的值为（ ）
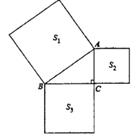A、7 B、8 C、9 D、104. 下列说法正确的是（ ）A、若 a、b、c是△ABC的三边，则a2＋b2＝c2 B、若 a、b、c是Rt△ABC的三边，则a2＋b2＝c2 C、若 a、b、c是Rt△ABC的三边， ，则a2＋b2＝c2 D、若 a、b、c是Rt△ABC的三边， ，则a2＋b2＝c25. 如图1，以直角三角形的各边为边分别向外作正三角形，再把较小的两张正三角形纸片按图2的方式放置在最大正三角形内．若知道图中阴影部分的面积，则一定能求出（ ）
A、直角三角形的面积 B、较小两个正三角重叠部分的面积 C、最大正三角形的面积 D、最大正三角形与直角三角形的面积差6. 如图，设小方格的面积为1，则图中以格点为端点且长度为 的线段有（ ）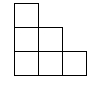
A、2条 B、3条 C、4条 D、5条7. 如图，点A坐标为（3，0），B是y轴正半轴上一点，AB=5，则点B的坐标为（ ）
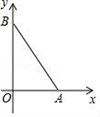A、（4，0） B、（0，4） C、（0，5） D、（0， ）8. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为（ ）
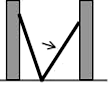A、2.2米 B、2.3米 C、2.4米 D、2.5米二、填空题
-
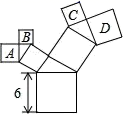
9. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为6cm，则正方形A，B，C，D的面积之和为cm2。
10. 生活经验表明：靠墙摆放梯子时，若梯子底端离墙约为梯子长度的 时，则梯子比较稳定．现有一长度为9 m的梯子，当梯子稳定摆放时，它的顶端能到达8.5 m高的墙头吗？(填“能”或“不能”)．11. 如图，分别以直角三角形各边为一边向三角形外部作正方形，其中两个正方形的面积分别为10 cm2和26 cm2 ， 则正方形A的边长是cm.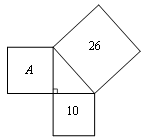
12. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”.他们仅仅少走了步路(假设2步为1米)，却踩伤了花草.
三、综合题
