内蒙古鄂尔多斯市2019-2020学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-08-26 类型:月考试卷
一、单选题
-
1. 下列函数关系中,不属于二次函数的是( )A、y=1﹣x2 B、y=(3x+2)(4x﹣3)﹣12x2 C、y=ax2+bx+c(a≠0) D、y=(x﹣2)2+22. 用配方法解3x2﹣6x=6配方得( )A、(x﹣1)2=3 B、(x﹣2)2=3 C、(x﹣3)2=3 D、(x﹣4)2=33. 把抛物线y=6(x+1)2平移后得到抛物线y=6x2 , 平移的方法可以是( )
A、沿y轴向上平移1个单位 B、沿y轴向下平移1个单位 C、沿x轴向左平移1个单位 D、沿x轴向右平移1个单位4. 若x=2是关于x的一元二次方程x2-mx+8=0的一个解.则m的值是( )A、6 B、5 C、2 D、-65. 已知(x2+y2+1)(x2+y2+3)=8,则x2+y2的值为( )A、-5或1 B、1 C、5 D、5或-16. 若抛物线y=x2﹣x﹣1与x轴的交点坐标为(m , 0),则代数式m2﹣m+2017的值为( )A、2019 B、2018 C、2017 D、20167. 如果关于x的一元二次方程k2x2-(2k+1)x+1=0有两个不相等的实数根,那么k的取值范围是( )A、k>- B、k>- 且 C、k<- D、k - 且8. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )A、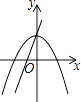 B、
B、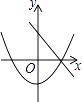 C、
C、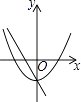 D、
D、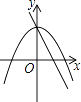 9. 已知方程x2+px+q=0的两个根分别是2和﹣3,则x2﹣px+q可分解为( )A、(x+2)(x+3) B、(x﹣2)(x﹣3) C、(x﹣2)(x+3) D、(x+2)(x﹣3)10. 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为x米,则可以列出关于x的方程是( )
9. 已知方程x2+px+q=0的两个根分别是2和﹣3,则x2﹣px+q可分解为( )A、(x+2)(x+3) B、(x﹣2)(x﹣3) C、(x﹣2)(x+3) D、(x+2)(x﹣3)10. 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为x米,则可以列出关于x的方程是( )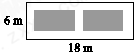 A、x2+9x-8=0 B、x2-9x-8=0 C、x2-9x+8=0 D、2x2-9x+8=0
A、x2+9x-8=0 B、x2-9x-8=0 C、x2-9x+8=0 D、2x2-9x+8=0二、填空题
-
11. 把方程3x(x﹣1)=(x+2)(x﹣2)+9化成ax2+bx+c=0的形式为 .12. 某公司举行年会晚宴,出席者两两碰杯一次,总共碰杯19900次,设晚宴共有x人参加,根据题意,可列方程 .13. 据调查,2011年5月兰州市的房价均价为7600元/m2 , 2013年同期将达到8200元/m2 , 假设这两年兰州市房价的平均增长率为x , 根据题意,所列方程为 .14. 在实数范围内定义一种运算“*”,其规则为a*b=a2﹣b2 , 根据这个规则,方程(x+2)*5=0的解为 .15. 已知A(﹣1,y1),B( ,y2),C(2,y3)三点都在二次函数y=﹣2x2的图象上,那么y1 , y2 , y3的大小关系是(用“<”连接) .16. 二次函数y=3x2+1和y=3(x﹣1)2 , 以下说法:
①它们的图象开口方向、大小相同;②它们的对称轴都是y轴,顶点坐标都是原点(0,1);③当x>0时,它们的函数值y都是随着x的增大而增大;④它们与坐标轴都有一个交点;其中正确的说法有 .
三、解答题
-
17. 用适当的方法解下列方程:(1)、(x﹣5)2=16(2)、x2=5x(3)、x2﹣4x+1=0(4)、x2+3x﹣4=018. 已知函数y=(x﹣1)2;自己画出草图,根据图象回答问题:(1)、求当﹣2≤x≤﹣1时,y的取值范围;(2)、求当0≤x≤3时,y的取值范围.19. 阅读下面的材料,回答问题:
解方程x4﹣5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y , 那么x4=y2 , 于是原方程可变为y2﹣5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=﹣1,x3=2,x4=﹣2.
(1)、在由原方程得到方程①的过程中,利用法达到的目的,体现了数学的转化思想.(2)、解方程(x2+x)2﹣4(x2+x)﹣12=0.20. 用配方法说明:无论x取何值,代数式x2﹣4x+5的值总大于0,再求出当x取何值时,代数式x2﹣4x+5的值最小?最小值是多少?21. 如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.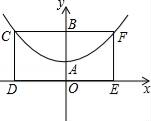 22. 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售价格降低多少元?23. 如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x﹣3=0的根,求平行四边形ABCD的周长.
22. 某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,在顾客得实惠的前提下,商家还想获得6080元的利润,应将销售价格降低多少元?23. 如图,平行四边形ABCD中,AE⊥BC于E,AE=EB=EC=a,且a是一元二次方程x2+2x﹣3=0的根,求平行四边形ABCD的周长.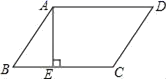 24. 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为ts,四边形APQC的面积为ymm2 .
24. 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,设运动的时间为ts,四边形APQC的面积为ymm2 .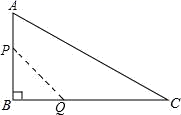 (1)、y与t之间的函数关系式;(2)、求自变量t的取值范围;(3)、四边形APQC的面积能否等于172mm2 . 若能,求出运动的时间;若不能,说明理由.
(1)、y与t之间的函数关系式;(2)、求自变量t的取值范围;(3)、四边形APQC的面积能否等于172mm2 . 若能,求出运动的时间;若不能,说明理由.