河北省石家庄市2019-2020学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-08-26 类型:月考试卷
一、单选题
-
1. 某同学在体育备考训练期间,参加了七次测试,成绩依次为(单位:分)51,53,56,53,56,58,56,这组数据的众数、中位数分别是( )A、53,53 B、53,56 C、56,53 D、56,562. 方差是刻画数据波动程度的量.对于一组数据 , , ,…, ,可用如下算式计算方差: ,其中“5”是这组数据的( )A、最小值 B、平均数 C、中位数 D、众数3. 把一元二次方程 化为一般形式,正确的是( )A、 B、 C、 D、4. 一元二次方程 的解为( )A、 B、x1=0,x2=4 C、x1=2,x2=-2 D、x1=0,x2=-45. 关于x的一元二次方程(m﹣1)x2+3x+m2﹣1=0的一根为0,则m的值是( )A、±1 B、±2 C、﹣1 D、﹣26. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差S2(单位:千克2)如下表所示:
甲
乙
丙
丁
x
24
24
23
20
S2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A、甲 B、乙 C、丙 D、丁7. 小韦和小黄进行射击比赛,各射击6次,根据成绩绘制的两幅折线统计图如下,以下判断正确的是( )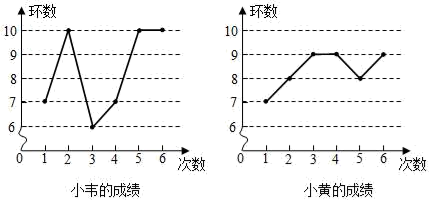 A、小黄的成绩比小韦的成绩更稳定 B、两人成绩的众数相同 C、小韦的成绩比小黄的成绩更稳定 D、两人的平均成绩不相同8. 小莹同学10个周综合素质评价成绩统计如下:
A、小黄的成绩比小韦的成绩更稳定 B、两人成绩的众数相同 C、小韦的成绩比小黄的成绩更稳定 D、两人的平均成绩不相同8. 小莹同学10个周综合素质评价成绩统计如下:成绩(分)
94
95
97
98
100
周数(个)
1
2
2
4
1
这10个周的综合素质评价成绩的中位数和方差分别是( )
A、97.5 2.8 B、97.5 3 C、97 2.8 D、97 39. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )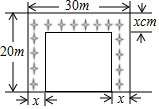 A、 B、 C、 D、10. 若 为方程 的一根, 为方程 的一根,且 都是正数,则 为( )A、5 B、6 C、 D、
A、 B、 C、 D、10. 若 为方程 的一根, 为方程 的一根,且 都是正数,则 为( )A、5 B、6 C、 D、二、填空题
-
11. 已知一组数据共有5个数,它们的方差是0.4,众数、中位数和平均数都是8,最大的数是9,则最小的数是.12. 学校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班的平均得分是分.
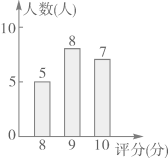 13. 用配方法解一元二次方程x2-mx=1时,可将原方程配方成(x-3)2=n,则m+n的值是 .14. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.15. 已知:一组自然数1,2,3…k,去掉其中一个数后剩下的数的平均数为16,则去掉的数是 .16. 已知a>b>0,且 ,则 =.
13. 用配方法解一元二次方程x2-mx=1时,可将原方程配方成(x-3)2=n,则m+n的值是 .14. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.15. 已知:一组自然数1,2,3…k,去掉其中一个数后剩下的数的平均数为16,则去掉的数是 .16. 已知a>b>0,且 ,则 =.三、解答题
-
17. 解下列方程(1)、2x2-x=0(2)、x2-4x=418. 某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
 19. 在“2019慈善一日捐”活动中,某校八年级(1)班40名同学的捐款情况如下表:
19. 在“2019慈善一日捐”活动中,某校八年级(1)班40名同学的捐款情况如下表:捐款金额(元)
20
30
50
a
80
100
人数(人)
2
8
16
x
4
7
根据表中提供的信息回答下列问题:
(1)、x的值为 ,捐款金额的众数为元,中位数为元.(2)、已知全班平均每人捐款57元,求a的值.20. 体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示. (1)、求女生进球数的平均数、中位数;(2)、投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?21. 某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)
(1)、求女生进球数的平均数、中位数;(2)、投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?21. 某农户承包荒山种了44棵苹果树.现在进入第三年收获期.收获时,先随意摘了5棵树上的苹果,称得每棵树摘得的苹果重量如下(单位:千克)35 35 34 39 37
(1)、在这个问题中,总体指的是?个体指的是?样本是?样本容量是?(2)、试根据样本平均数去估计总体情况,你认为该农户可收获苹果大约多少千克?22. 学校为奖励“汉字听写大赛”的优秀学生,派王老师到商店购买某种奖品,他看到如表所示的关于该奖品的销售信息,便用1400元买回了奖品,求王老师购买该奖品的件数.购买件数
销售价格
不超过30件
单价40元
超过30件
每多买1件,购买的所有物品单价将降低0.5元,但单价不得低于30元
23. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场平均每天可多售出2件,每件商品降价多少元时,商场日盈利可到达2100元?24. 随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区 年 月 日—— 年 月 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.收集数据
朝阳区
南关区
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量
优
良
轻微污染
中度污染
重度污染
朝阳区
南关区
(说明:空气质量指数 时,空气质量为优; 空气质量指数 时,空气质量为良; 空气质量指数 时,空气质量为轻微污染; 空气质量指数 时,空气质量为中度污染; 空气质量指数 时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区
平均数
中位数
方差
朝阳区
南关区
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.
25. 四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?(3)、若该专卖店打算每天获利至少2240元,请你直接写出每千克核桃售价m的取值范围 .