山西省晋中市平遥县2019-2020学年八年级上学期数学第三次月考试卷
试卷更新日期:2020-08-26 类型:月考试卷
一、单选题
-
1. 的值是( )A、0 B、 C、1 D、-12. 多项式 中各项的公因式是( )A、 B、 C、 D、23. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、
 B、
B、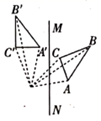 C、
C、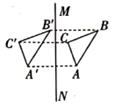 D、
D、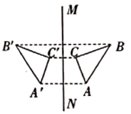 4. 下列计算正确的是( )A、 B、 C、 D、5. 用简便方法计算,将 变形正确的是( )A、 B、 C、 D、6. 已知 , ,则代数式 的值为( )A、36 B、26 C、20 D、167. 如图,在等边 中, 是 的中点, 于点 , 于点 ,已知 ,则 的长为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 用简便方法计算,将 变形正确的是( )A、 B、 C、 D、6. 已知 , ,则代数式 的值为( )A、36 B、26 C、20 D、167. 如图,在等边 中, 是 的中点, 于点 , 于点 ,已知 ,则 的长为( ) A、3 B、4 C、5 D、68. 已知 ,求 的值时,下面是两位同学的解法:甲:∵ ,∴ , , ,∴ .乙:对于 来说,当 时, ,∴只要把 代入等号的左右两边,得到 .对于这两位同学的解法下列说法正确的是( )A、只有甲对 B、只有乙对 C、两者都不对 D、两者都对9. 学了多项式乘多项式后,老师设计一接力游戏,用合作的方式完成下题.规定:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一个,最终完成这个题目.过程如下:接力中,自己负责的一步出现错误的是( )
A、3 B、4 C、5 D、68. 已知 ,求 的值时,下面是两位同学的解法:甲:∵ ,∴ , , ,∴ .乙:对于 来说,当 时, ,∴只要把 代入等号的左右两边,得到 .对于这两位同学的解法下列说法正确的是( )A、只有甲对 B、只有乙对 C、两者都不对 D、两者都对9. 学了多项式乘多项式后,老师设计一接力游戏,用合作的方式完成下题.规定:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一个,最终完成这个题目.过程如下:接力中,自己负责的一步出现错误的是( ) A、甲 B、乙 C、丙 D、丁10. 如图,等腰 的面积为9,底边 的长为3,腰 的垂直平分线 分别交 、 边于点 、 ,点 为 边的中点,点 为直线 上一动点,则 的最小值为( )
A、甲 B、乙 C、丙 D、丁10. 如图,等腰 的面积为9,底边 的长为3,腰 的垂直平分线 分别交 、 边于点 、 ,点 为 边的中点,点 为直线 上一动点,则 的最小值为( ) A、12 B、9 C、6 D、3
A、12 B、9 C、6 D、3二、填空题
-
11. 因式分解: .12. 如图,在 中, , 、 分别是 、 上的点, , , , ,则 的长为.
 13. 若实数a,b满足a﹣2b=4,ab=2,那么a2+4b2=.14. 如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=度.
13. 若实数a,b满足a﹣2b=4,ab=2,那么a2+4b2=.14. 如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=度. 15. 若 ,则 的值为.
15. 若 ,则 的值为.三、解答题
-
16. 计算:(1)、 ;(2)、 .17. 先化简,再求值: ,其中 .18. 如图,在四边形 中, 垂直平分 , 垂直平分 .
 (1)、求证: .(2)、若 ,求 的度数.19. 如图,在四边形 中, , , , , ,求 的长.
(1)、求证: .(2)、若 ,求 的度数.19. 如图,在四边形 中, , , , , ,求 的长. 20. 甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2-7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x-3.(1)、求a,b的值;(2)、请计算这道题的正确结果21. 如图, 是等边三角形, 、 分别是 、 边上的点,连接 、 ,且 、 相交于点 , .
20. 甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2-7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x-3.(1)、求a,b的值;(2)、请计算这道题的正确结果21. 如图, 是等边三角形, 、 分别是 、 边上的点,连接 、 ,且 、 相交于点 , . (1)、求 的度数.(2)、过点 作 于 ,若 , ,求 的长.22. 如图所示的两个长方形用不同方式拼成图1和图2两个图形.
(1)、求 的度数.(2)、过点 作 于 ,若 , ,求 的长.22. 如图所示的两个长方形用不同方式拼成图1和图2两个图形. (1)、若图1中的阴影部分的面积用大正方形减去小正方形表示为 ,则图2中的阴影部分的面积用长乘以宽可表示为.(用含字母 、 的代数式表示)(2)、由(1)可以得到等式.(3)、根据所得到的等式解决下面的问题:
(1)、若图1中的阴影部分的面积用大正方形减去小正方形表示为 ,则图2中的阴影部分的面积用长乘以宽可表示为.(用含字母 、 的代数式表示)(2)、由(1)可以得到等式.(3)、根据所得到的等式解决下面的问题:①计算: .
②解方程: .
23. 阅读理解:我们知道,比较两数(式)大小有很多方法,“作差法”是常用的方法之一,其原理是不等式(或等式)的性质:若 ,则 ;若 ,则 ;若 ,则 .例:已知 , ,其中 ,求证: .
证明: .
∵ ,∴ ,∴ .
(1)、操作感知:比较大小:①若 ,则 ;
② .
(2)、类比探究:已知 , ,试运用上述方法比较 、 的大小,并说明理由.(3)、应用拓展:已知 , 为平面直角坐标系中的两点,小明认为,无论 取何值,点 始终在点 的上方,小明的猜想对吗?为什么?