高中数学人教新课标A版选修2-1 2.2椭圆

试卷更新日期：2020-08-26 类型：同步测试

进入出卷网下载

一、单选题

1. 已知 $F_{1}$ ､ $F_{2}$ 是定点， $| F_{1} F_{2} | = 6$ .若动点M满足 $| M F_{1} | + | M F_{2} | = 6$ ，则动点M的轨迹是（）

A、直线 B、线段 C、圆 D、椭圆

查看试题解析
2. 椭圆 $\frac{x^{2}}{m} + \frac{y^{2}}{4} = 1$ 的焦距是2，则m的值是（）

A、5 B、5或8 C、3或5 D、20

查看试题解析
3. 设集合 $A = {1 ， 2 ， 3 ， 4}$ ， $m ， n \in A$ ，则方程 $\frac{x^{2}}{m} + \frac{y^{2}}{n} = 1$ 表示焦点位于x轴上的椭圆有（）

A、6个 B、8个 C、12个 D、16个

查看试题解析
4. 对于椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ ，下面说法正确的是（）

A、长轴长为2 B、短轴长为3 C、离心率为 $\frac{1}{2}$ D、焦距为1

查看试题解析
5. 设 $M$ 是椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ 上的任意一点，若 $F_{1}, F_{2}$ 是椭圆的两个焦点，则 $| M F_{1} | + | M F_{2} |$ 等于（）

A、 $2$ B、 $3$ C、4 D、6

查看试题解析
6. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{1}{2}$ ，且椭圆C的长轴长与焦距之和为6，则椭圆C的标准方程为 $($ $)$

A、 $\frac{4 x^{2}}{25} + \frac{y^{2}}{6} = 1$ B、 $\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$ C、 $\frac{x^{2}}{2} + y^{2} = 1$ D、 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$

查看试题解析
7. 若曲线 $\frac{x^{2}}{1 - k} + \frac{y^{2}}{1 + k} = 1$ 表示椭圆，则 $k$ 的取值范围是（）

A、 $k > 1$ B、 $k < - 1$ C、 $- 1 < k < 1$ D、 $- 1 < k < 0$ 或 $0 < k < 1$

查看试题解析
8. 已知椭圆 $M (1 ， 0)$ 分别过点 $A (2 ， 0)$ 和点 $B (1 ， \frac{\sqrt{3}}{2})$ ，则该椭圆的焦距为（）

A、 $\sqrt{3}$ B、2 C、 $2 \sqrt{3}$ D、 $2 \sqrt{5}$

查看试题解析
9. 设 $F_{1}$ ､ $F_{2}$ 分别是椭圆 $E : x^{2} + \frac{y^{2}}{b^{2}} = 1$ ( $0 < b < 1$ )的左､右焦点，过 $F_{1}$ 的直线 $l$ 与椭圆E相交于A､B两点，且 $2 | A B | = | A F_{2} | + | B F_{2} |$ ，则 $| A B |$ 的长为（）

A、 $\frac{2}{3}$ B、1 C、 $\frac{4}{3}$ D、 $\frac{5}{3}$

查看试题解析
10. 已知 $F_{1}$ 、 $F_{2}$ 为椭圆 $C$ ： $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 的左、右焦点，过点 $F_{2}$ 作斜率为 $1$ 的直线 $l$ 与 $C$ 交于 $A$ 、 $B$ 两点，则 $Δ A B F_{1}$ 的面积为（）

A、 $\frac{12 \sqrt{2}}{7}$ B、 $\frac{6 \sqrt{2}}{7}$ C、 $\frac{12}{7}$ D、 $\frac{12 \sqrt{3}}{7}$

查看试题解析
11. 已知点F是椭圆 $\frac{y^{2}}{a^{2}} + \frac{x^{2}}{b^{2}} = 1 (a > b > 0)$ 的上焦点，点P在椭圆E上，线段PF与圆 $x^{2} + {(y - \frac{c}{2})}^{2} = \frac{b^{2}}{16}$ 相切于点Q，O为坐标原点，且 $(\vec{O P} + \vec{O F}) \cdot \vec{F P} = 0$ ，则椭圆E的离心率为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
12. 过原点的一条直线与椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 交于A，B两点， $F_{2}$ 为椭圆右焦点，且AB长度等于焦距长，若 $∠ A B F_{2} \in (\frac{π}{12} ， \frac{5 π}{12})$ ，则该椭圆离心率的取值范围为（）

A、 $(\frac{\sqrt{2}}{2} ， 1)$ B、 $[\frac{\sqrt{2}}{2} ， \frac{\sqrt{6}}{3})$ C、 $(\frac{\sqrt{6}}{3} ， 1)$ D、 $(\frac{\sqrt{2}}{2} ， \frac{\sqrt{3}}{2})$

查看试题解析

二、多选题

13. 1970年4月24日，我国发射了自己的第一颗人造地球卫星“东方红一号”，从此我国开始了人造卫星的新篇章.人造地球卫星绕地球运行遵循开普勒行星运动定律：卫星在以地球为焦点的椭圆轨道上绕地球运行时，其运行速度是变化的，速度的变化服从面积守恒规律，即卫星的向径（卫星与地球的连线）在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为 $2 a$ ， $2 c$ ，下列结论正确的是（）

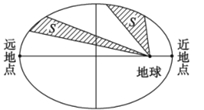A、卫星向径的取值范围是 $[a - c ， a + c]$ B、卫星在左半椭圆弧的运行时间大于其在右半椭圆弧的运行时间 C、卫星向径的最小值与最大值的比值越大，椭圆轨道越扁 D、卫星运行速度在近地点时最大，在远地点时最小

查看试题解析

三、填空题

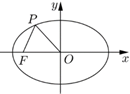
14. 已知点M( $\sqrt{3}$ ，0)，椭圆 $\frac{x^{2}}{4} + y^{2} = 1$ 与直线y＝k(x＋ $\sqrt{3}$ )交于点A，B，则△ABM的周长为.

查看试题解析
15. 如图，已知椭圆C的中心为原点O， $F (- 2 \sqrt{5} ， 0)$ 为椭圆C的左焦点，P为椭圆C上一点，满足 $| O P | = | O F |$ 且 $| P F | = 4$ ，则椭圆C的标准方程为.

查看试题解析
16. 直线 $y = \frac{\sqrt{3}}{3} x$ 与椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 交于A､B两点，F为椭圆的右焦点，若 $A F ⊥ B F$ ，则椭圆的离心率为.

查看试题解析
17. 设 $F_{1}$ ， $F_{2}$ 是椭圆 $C ： \frac{x^{2}}{4} + y^{2} = 1$ 的两个焦点，过 $F_{1}$ 的直线 $l_{1}$ 与椭圆C交于A，B两点，过 $F_{2}$ 与 $l_{1}$ 平行的直线 $l_{2}$ 与椭圆C交于C，D两点（点A，D在x轴上方），则四边形 $A B C D$ 面积的最大值为.

查看试题解析

四、解答题

18. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点M（2，3），点A为其左顶点，且AM的斜率为 $\frac{1}{2}$ ，

(1)、求C的方程；

(2)、点N为椭圆上任意一点，求△AMN的面积的最大值.

查看试题解析
19. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ，且过点A（2，1）．

(1)、求C的方程：

(2)、点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

查看试题解析
20. 已知：椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦距为2，且经过点 $M (1, \frac{3}{2})$ ，A､B是椭圆上异于M的两个动点.

(1)、求椭圆C的方程；

(2)、若 $∠ A M B = 90 °$ ，求证：直线 $A B$ 过定点，并求出该定点坐标.

查看试题解析
21. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的一个顶点为 $A (0, - 3)$ ，右焦点为F，且 $| O A | = | O F |$ ，其中O为原点．
（Ⅰ）求椭圆的方程；

（Ⅱ）已知点C满足 $3 \vec{O C} = \vec{O F}$ ，点B在椭圆上（B异于椭圆的顶点），直线 $A B$ 与以C为圆心的圆相切于点P，且P为线段 $A B$ 的中点．求直线 $A B$ 的方程．

查看试题解析
22. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 过点 $A (- 2, - 1)$ ，且 $a = 2 b$ ．
（Ⅰ）求椭圆C的方程：

（Ⅱ）过点 $B (- 4, 0)$ 的直线l交椭圆C于点 $M, N$ ,直线 $M A, N A$ 分别交直线 $x = - 4$ 于点 $P, Q$ ．求 $\frac{| P B |}{| B Q |}$ 的值．

查看试题解析
23. 已知椭圆 $Γ : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ ( $a > b > 0$ )的焦距为2，椭圆 $Γ$ 的左､右焦点分别为 $F_{1}$ ､ $F_{2}$ ，过右焦点 $F_{2}$ 作x轴的垂线交椭圆于A､B两点， $| A B | = 3$ .

(1)、求椭圆 $Γ$ 的方程；

(2)、过右焦点 $F_{2}$ 作直线交椭圆于C､D两点，若△ $C D F_{1}$ 的内切圆的面积为 $π$ ，求△ $C D F_{1}$ 的面积；

(3)、已知 $⊙ O : x^{2} + y^{2} = b^{2}$ ， $R$ 为圆上一点(R在y轴右侧)，过R作圆的切线交椭圆 $Γ$ 于M､N两点，试问△ $M N F_{2}$ 的周长是否为一定值？若是，求出该定值，若不是，请说明理由.

查看试题解析

高中数学人教新课标A版 选修2-1 2.2椭圆

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教新课标A版选修2-1 2.2椭圆